I have been studying theta-functions and made an interesting observation which I have a question about
QUESTION: Is there a more intuitive, in particular a mostly geometric way, to prove the four square theorem which is based on Integral Apollonian Circle Packings? Alternatively, is there an "intuitive" proof of the four square theorem which does not involve the theta function or other analytic "heavy machinery" but is more elementary or geometric in nature?
Motivation: It's well known that any positive integer can be represented as the sum of at most 4 squares. It's less well known, that any 4 integers form the basis for an Integral Apollonian Circle Packing. It turns out that it's possible to use the theta-function to prove the four square theorem in a very direct way (see Shakarchi Stein Vol 2, Chapter 10); I understand the proof but it feels like there is some geometric intuition that is being lost in this process.
To see the connection between the theta-function, the four square theorem, and Apollonian circle packing; we can make use of the following rule: given any 4 integers $a,b,c,d \in \mathbb{Z}$ $$ bc - ad = 1 $$
The theta-function has a functional equation which is based on this rule, and this rule forms the basis for the Integral Apollonian Circle packing method. These types of results are also directly related to the "Gauss Map" and provide a recipe for using dynamical systems theory to study continued fraction expansions.
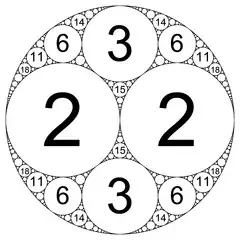
Update (further motivation): I am reading this paper Apollonian Circle Packings: Number Theory II. Spherical and Hyperbolic Packings. I was led to these types of circle packings a couple of months ago after I learned about the Descartes circle theorem and the the Descartes quadratic form. One way to restate the condition of Integral Circle Packings is by using the "four-dimensional metric"
$$2(a^2 + b^2 + c^2 + d^2)^2 - (a + b + c + d)^2 = 0$$
The observation is that this quadratic form is of the same type as a condition in probability theory for the definition of the expected value of a random variable. This also provides an intuitive connection, at least for me, to the theory of lie algebra's which dominate the higher theory of these types of integral circle packings and their representations, because I imagine this quadratic form is a commutator between some kind of strange mathematical object I am struggling to understand
(Note: please provide any feedback about how I can do a better job of posing these types of abstract questions, I struggle to communicate these types of idea's sometimes, and am working hard on improving my exposition. Any advice or suggestions are much appreciated.)