0

I am trying to graph 1 number against 2. I need a way to condense those 2 numbers into 1. It is not necessary to retrieve those numbers back, only that the number coded from (b,c) is unique from any other pair of numbers applied in this algorithm.

Bonus to an algorithm that keeps the coded X small and manageable.

SumsArentDumb
  • 47
  • 1
    So what you want is a bijective function $f : \Bbb R^2 \to \Bbb R$. Such bijections do exist, though none come to mind at the moment... – PrincessEev Apr 04 '20 at 21:12
  • 1
    You could interleave the binary digits... – kimchi lover Apr 04 '20 at 21:13
  • @EeveeTrainer It doesn't need to be surjective and I'm more looking for a method or algorthm rather than a function in the traditional sense – SumsArentDumb Apr 04 '20 at 21:26
  • See here. Or you can use the inverse of a space filling curve to get it continuous. @EeveeTrainer OP only asks for an objective function it seems. So some bijective constructions can probably be simplified somewhat. – Milten Apr 04 '20 at 21:26
  • 1
    What is the purpose of the graph? Encoding two numbers into one is going to be unhelpful for graphing purposes. – Somos Apr 04 '20 at 23:53
  • @Somos The graph is useful for allowing me to easily record and get a general idea of which values of a,b,c generate of bounded sequence under a particular algorithm. If it does, I mark it on the 2d graph under (a, f(b,c)). 'a' is more important to the result than b and c. There are many cases to check to just remember and I just don't have any useful means to record it in a 3d space. – SumsArentDumb Apr 05 '20 at 00:07
  • 1
    Anything special about the numbers b and c? Are they always positive? Are they always integers? Are they always contained in some range of values? – Wilf Rosenbaum Apr 05 '20 at 02:26
  • I think you need to give a lot more pertinent details in order to get a useful answer. – Somos Apr 05 '20 at 11:22

1 Answers1

1

As kimchi lover (nice name :)) suggests, I think interleaving digits is a good and practical method. That means we get an injection $f:(0,1)^2\to(0,1)$ by: $$ f:(x,y) = (0.a_1a_2a_3\!\ldots, 0.b_1b_2b_3\!\ldots) \mapsto 0.a_1b_1a_2b_2a_3b_3\!\ldots $$ This is unique (i.e. well-defined) and injective, if we choose a convention for numbers with repeating 9's or 0's. It is practical, because we can just take however many digits we want.

This is easily transformed to an injection $\mathbb R^2\to \mathbb R$ by using a bijection $(0,1)\to\mathbb R$, say $g:x\mapsto \log\left(\frac1x-1\right)$. Then we have: $$ h(x,y) := g\circ f\big(g^{-1}(x),g^{-1}(y)\big) $$ is an injection $\mathbb R^2\to\mathbb R$.

Note that this method can be made bijective as shown in this answer.

EDIT: I realised that we can easily extend $f$ to $\mathbb R_+^2 \to \mathbb R_+$ like this: $$ f:(x,y) = (\ldots\!A_2A_1.a_1a_2\!\ldots, \ldots\!B_2B_1.b_1b_2b_3\!\ldots) \mapsto \ldots\! A_2B_2A_1B_1.a_1b_1a_2b_2\!\ldots $$ For example $f(1.23,456.789) = 40516.273809$. I don't see an immediate extension to the whole plain, other than doing a similar trick as before with a bijective function $\mathbb R_+\to \mathbb R$.

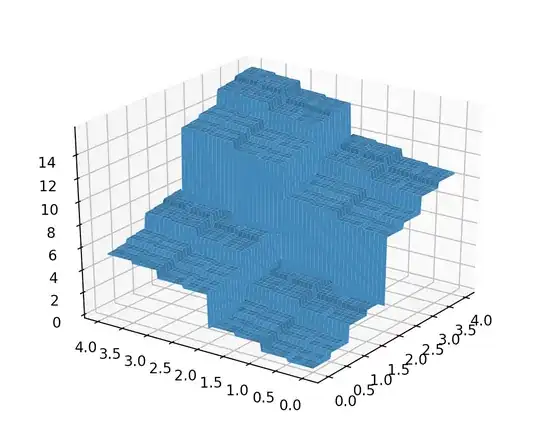
I went ahead and plotted $f$. I quite like the fractal shape, combined with nice regularity! This is honestly a nicer function than I would have thought would be easy to find. I can share the (unpolished) code, if you want. In decimal:

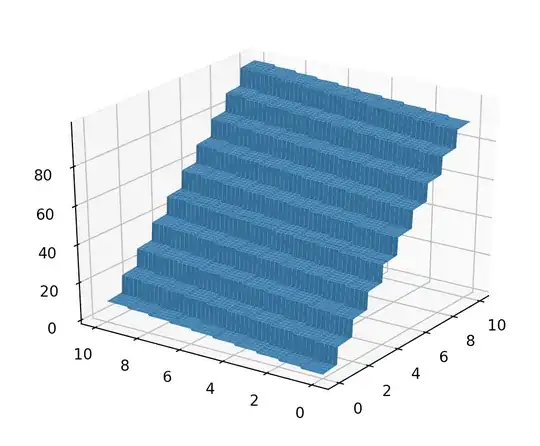
In binary: enter image description here

Milten
  • 7,722