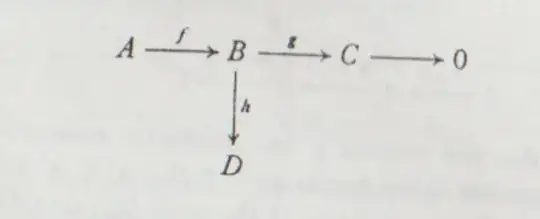1

Here is the picture of the sequence

I have the next sequence where the row is exact, A, B, C and D are $R$-Modules and $ h \circ f =0$. I need to prove that exists a homomorphism $k: C \to D$ uniquely determined such that $ k \circ g = h$

erika21148
  • 449
  • You might check out my answer to your other question https://math.stackexchange.com/questions/3607250/proof-about-exact-sequence. Cheers! – Robert Lewis Apr 04 '20 at 03:40

1 Answers1

2

$h$ "factors through" $g$. This is completely analogous to the first isomorphism theorem.

Given $c\in C$, define $k(c)=h(b)$, where $b$ is any element of $g^{-1}(c)\ne\emptyset$. One can check that this is a well defined homomorphism, using the exactness.

I think you could probably call this a "universal property of exact sequences". It could also probably be phrased in terms of "uniqueness of final objects" in category theory, but I am not prepared to do that right now.