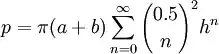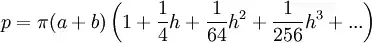1

I am by no means a math buff but I am trying to implement a reasonable accurate formula for calculating the perimeter of an ellipse for a program I am writing.

I found a web page that offers a few formulae and I am interested in this one:

enter image description here

I have no idea how a "binomial coefficient" works, I am only interested in how I can determine the denominator for n number of terms. Ex:

enter image description here

Here there are 3 "terms", how did the writer of the article determine that 4, 64 and 256 are appropriate denominators?

I noticed that 4 = 1 *4, 64 = 4 * 4 * 4, 256 = 4 * 4 * 4 * 4 and so forth.

My code so far:

for(let i = 1; i <= iterations; i++)
    if(i == 1)
        rh += (1/4) * h;
    else
        rh += (1/(Math.pow(4, i+1)))*Math.pow(h, i);

I would like to avoid the if-else statement if possible.

Matthew Goulart
  • 111

2 Answers2

2

There is unforunately no “and so forth” here; this is an example of the dangers of generalizing from patterns in a few (or sometimes even many) examples. (In this case, there wasn’t even a pattern extending over $3$ examples; you created one by making an exception for one of the three).

When the lower index of the binomial coefficient $\binom nk$ is a non-negative integer, it takes the value

$$ \frac{n(n-1)\cdots(n-k+1)}{k!}\;. $$

So the first few values of $\binom{\frac12}n$ are

\begin{eqnarray} \binom{\frac12}0&=&\frac1{0!}=1\;,\\ \binom{\frac12}1&=&\frac{\frac12}{1!}=\frac12\;,\\ \binom{\frac12}2&=&\frac{\frac12\left(-\frac12\right)}{2!}=-\frac18\;,\\ \binom{\frac12}3&=&\frac{\frac12\left(-\frac12\right)\left(-\frac32\right)}{3!}=\frac1{16}\;,\\ \binom{\frac12}4&=&\frac{\frac12\left(-\frac12\right)\left(-\frac32\right)\left(-\frac52\right)}{4!}=-\frac5{128}\;. \end{eqnarray}

So it just so happens that the absolute value of three consecutive of these coefficients is an inverse power of two (and hence the square is a power of four), but this pattern doesn’t continue. You’ll need to calculate the coefficients according to the definition.

joriki
  • 242,601
0

In case if you are happy with an approximation that gives an error of order $h^5$. Following is the formula: $$\ p \approx \pi(a+b)(1+\frac{3h}{10+\sqrt{4-3h}}) $$

Shiv Tavker
  • 1,652