1

This exercise is from a Complex Analysis course, more explicitly inside the "Laplce Transform" chapter:

Find a reduction for $$(H(t+3)-H(t-5))\cdot(\delta(t+2)+\delta(t-3)+\delta(t-9)),$$ where $H(t)$ is the Heaviside function: $$H(t-a)=\begin{cases}1,&t>a,\\0,&t<a,\end{cases}$$ and $\delta(t)$ is the Dirac function: $$\delta(t)=\lim_{\tau\to0}F_{\delta}(t),\quad F_{\delta}(t)=\begin{cases}1/\tau,&0\leq t<\tau\\0,&t>\tau.\end{cases}$$

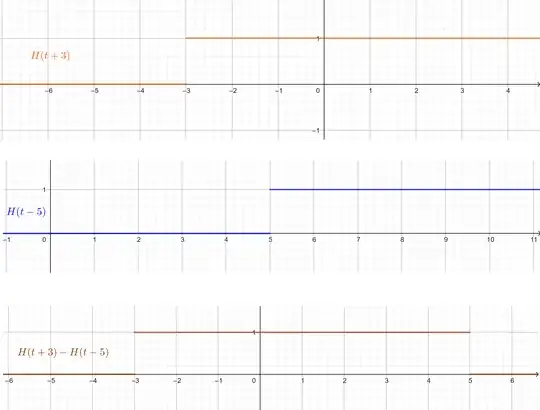
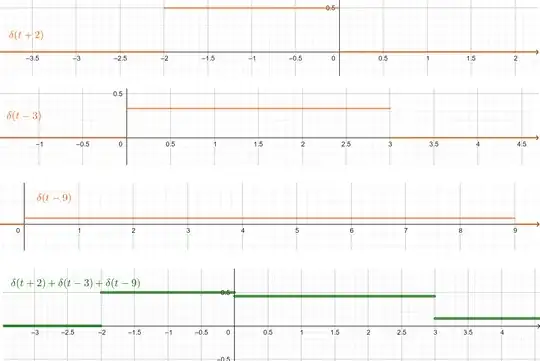
I plotted the functions:

$H(t+3)-H(t-5)$:

Heaviside functions graph

$\delta(t+2)+\delta(t-3)+\delta(t-9)$:

Dirac functions graph

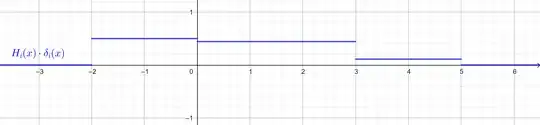
Finally, the answer would be $(H(t+3)-H(t-5))\cdot(\delta(t+2)+\delta(t-3)+\delta(t-9))$:

Graph of the answer

As an expression:

$$ (H(t+3)-H(t-5))\cdot(\delta(t+2)+\delta(t-3)+\delta(t-9))= \begin{cases} 0,&x<-2,\\ 1/2,&-2\leq x<0,\\ 4/9,&0\leq x<3,\\ 1/9,&3\leq x<5,\\ 0,&x>5. \end{cases} $$

Is this right? What other method would you use to find the product?

Leucippus
  • 27,174
manooooh
  • 2,299

2 Answers2

1

Using sifting property of delta function: $$\int_{-\infty}^{+\infty}(H(t+3)-H(t-5))(\delta(t+2)+\delta(t-3)+\delta(t-9))dt$$

$$ = \int_{-\infty}^{+\infty} H(1)\delta(t+2)dt - \int_{-\infty}^{+\infty}H(-7)\delta(t+2)dt +$$ $$\int_{-\infty}^{+\infty}H(6)\delta(t-3)dt - \int_{-\infty}^{+\infty}H(-2)\delta(t-3)dt + $$ $$\int_{-\infty}^{+\infty}H(12)\delta(t-9)dt - \int_{-\infty}^{+\infty}H(4)\delta(t-9)dt = 2$$

S.H.W
  • 4,462
  • Thanks for the answer!! Why do you use integrals if I am asking for a rearrangement of Heaviside and Dirac functions? – manooooh Mar 29 '20 at 17:26
  • 1
    @manooooh You're welcome. Please see the following link. I think it will be helpful. https://math.stackexchange.com/questions/1947782/why-does-the-dirac-delta-function-satisfy-fx-deltax-a-fa-deltax-a – S.H.W Mar 29 '20 at 19:07
  • The problem is, I think, we are not speaking in the same language. The definition of $\delta(x)$ is not the same as the definition of $\delta(x)$ I am proposing. The definition that we have to use is in this question. – manooooh Mar 29 '20 at 19:26
  • @manooooh $\delta(x)$ is in fact a generalized function. – S.H.W Mar 29 '20 at 19:46
  • But do we agree that both your and my final answer differ? – manooooh Mar 29 '20 at 20:35
1

The singularities of the step functions that appear in the problem are at $t=-3$ and $t=+5$. The singularities of the delta functions are at $t=-2$, $t=+3$ and $t=+9$, which fortunately are different than the previous ones. Therefore we can multiply these distributions without problem. For example $H(t+3)\delta(t+2)=\delta(t+2)$ because at $t=-2$ we have that $H(t+3)$ equals one. Similarly, $H(t-5)\delta(t-3)=0$ because at $t=3$ we have that $H(t-5)$ equals zero. So simplifying we have:

$$ \begin{align} (H(t+3)−H(t−5))⋅(\delta(t+2)+\delta(t−3)+\delta(t−9))&=\\ \delta(t+2)+\delta(t−3)+\delta(t−9)-\delta(t−9)&=\\ \delta(t+2)+\delta(t−3) \end{align}$$

Anders Beta
  • 1,193
  • 5
  • 11
  • It equals to $\delta(t+2)+\delta(t−3)+\delta(t−9)$. The term $-\delta(t−9)$ is wrong. – S.H.W Mar 29 '20 at 03:57
  • $H(t+3)\delta(t-9)=\delta(t-9)$ and $-H(t-5)\delta(t-9)=-\delta(t-9)$, so both cancel in the final answer. – Anders Beta Mar 29 '20 at 05:21
  • You're right, sorry for that. – S.H.W Mar 29 '20 at 06:07
  • Thanks @AndersBeta! Could you state your answer by considering the context of a basic Complex Analysis course, please? I mention this because you wrote "these distributions" and we don't focus on Probability. Also, why is my answer wrong? Thank you. – manooooh Mar 29 '20 at 17:32
  • By distributions I do not mean probability distributions but Schwartz type distributions (also called generalized functions). You may have to look at some references to learn more about them. You could stat in some of the Wikipedia pages that describe them, like the pages on the "Dirac delta function" or "Distribution (mathematics)" and follow the references. I do not know how they appear in your complex analysis course, it does not seem to me like the most appropriate place to discuss them. – Anders Beta Mar 29 '20 at 20:11
  • But do we agree that both your and my final answer differ? – manooooh Mar 29 '20 at 20:35
  • 1
    Yes. Your final answer is completely incorrect. Your plots of the delta functions show that you do not have a grasp of what the delta "function" is. Remember that $\delta(t-t_0)$ is zero at all points except at $t=t_0$ (where is infinite). – Anders Beta Mar 29 '20 at 20:40
  • Oh, that's right. So what answer should I mark as correct? Your answer is $\delta(t+2)+\delta(t-3)$, but @S.H.W says $2$. Thanks. – manooooh Mar 31 '20 at 00:12
  • $2$ is not correct either. That $2$ is the integral of the final answer, $\delta(t+2)+\delta(t-3)$. I do not know why S.H.W. computes the integral, because the problem only asks to find a reduction of the original expression, not its integral. BUT YOU SHOULD NOT MARK IT CORRECT BECAUSE I SAY SO, ONLY WHEN YOU FULLY UNDERSTAND WHY IS CORRECT. – Anders Beta Mar 31 '20 at 00:53