Distributing Series/Patterns

Question

I'm going to do my best to explain this question, but it's complicated. Please bear with me. I'm trying to solve a practical problem and I know that the answer involves some math, but I can't for the life of me figure it out.

You've got a series of hexagons, and each side is numbered with a digit, 0 through 5, like this:

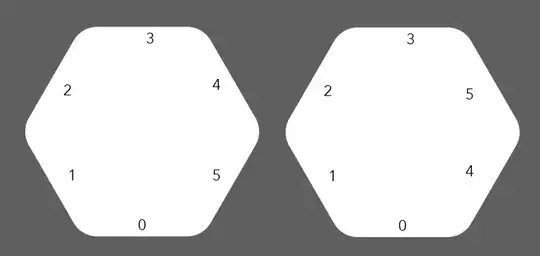
image of hexagons with numbered sides

If you give each hexagon a unique sequence of the digits 0 to 5 (i.e., 0-1-2-3-4-5, 0-1-2-3-5-4, 0-1-2-4-3-5, etc.), you'll get 120 unique hexagons. Here are all the combinations:

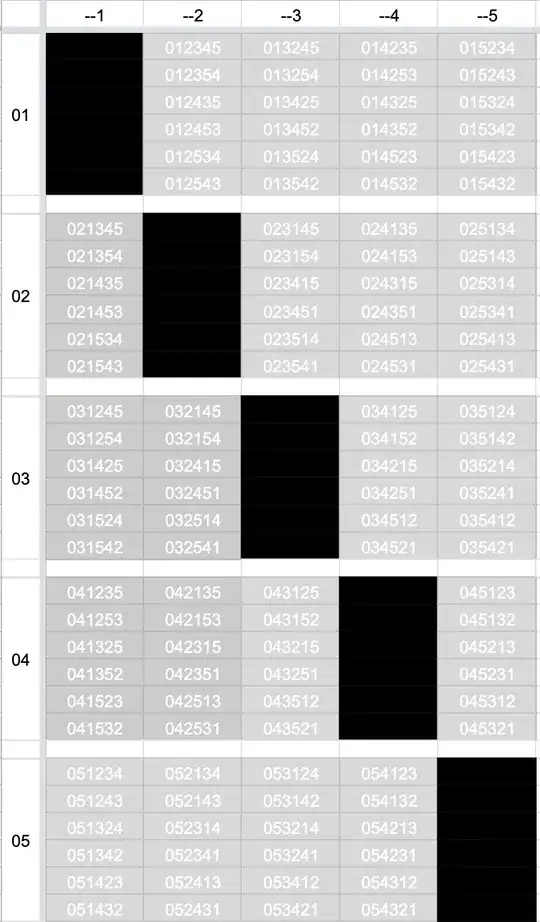
table of all 0-5 sequences

(The sequence loops around the hexagon, so for my purposes 0-1-2-3-4-5, 1-2-3-4-5-0, 2-3-4-5-0-1 are all the same sequence. I set them all to starting with 0 for simplicity's sake.)

When you've got the full list of these 6-digit sequences typed out, any 3-digit combination of those numerals occurs exactly 6 times as a subsequence. 1-2-3 occurs 6 times. 4-1-2 occurs 6 times. Etc.

So, we have 120 different hexagons, each with a unique sequence on it. I am going to label each one with a letter, A to F, like this:

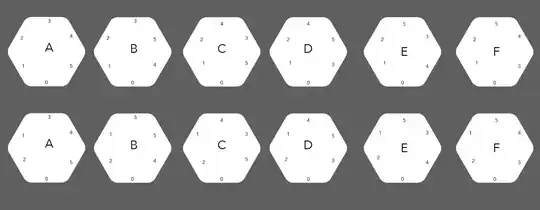
image of 12 hexagons, each with a unique sequence of numbers at the edges. The hexagons are labeled A-B-C-D-E-F, A-B-C-D-E-F

So, there are 6 letters and 6 instances of each 3-digit subsequence. What I want to do is distribute the letter labels among the 120 unique hexagons in such a way that each of those letter labels coincides with each 3-digit combination exactly once. That is, if you were to find the 6 hexagons that contain a 4-1-6 sequence, each letter would be different. If you found the 6 3-2-1 hexagons, each letter would be different, and so on.

My intuition tells me that this is possible, but I cannot figure out how to make this happen. Help!!

What's preventing you from doing an exhaustive search? For instance, search all 120 hexagons one by one for 012, each time you see a new hexagon with 012 you add a new letter to it. Then repeat for 013... etc. Does this not work? — Ben10, Mar 27 '20 at 18:34
Ah, good question. That was my first instinct, too, and I thought it would be simple. What complicates it is this: You go and label the 6 different sequences that contain 0-1-2 with your letters, but each of those sequences also contains other subsequences. So, when you're labeling 0-1-2-4-3-5 with an A, you are not assigning that A only to the 0-1-2; it's also getting assigned to 1-2-4, 2-4-3, 4-3-5, and 3-5-0. This becomes unmanageably complex to figure out (even with the ridic spreadsheet I've set up). — Ginseng English, Mar 27 '20 at 18:45
@Rob There are only chatrooms here. If we keep adding comments here by replying to each other, a link to a new one will appear automatically at some point and will tell us to continue our conversation there. I'm fine with using that. If you want to use any other way of communicating such as exchanging emails that's also fine. — Vepir, Apr 05 '20 at 10:12

Vepir · Accepted Answer · 2020-04-04T13:07:37.823

I've ran an exhaustive search (as Ben10's comment suggests) and the first solution was found after around $3\cdot10^5$ potential solution paths were discarded. Below is the found solution.

The labeled hexagon permutations, sorted in two different ways:

Sorted by permutations:      Sorted by labels:
([0, 1, 2, 3, 4, 5], 'A')    ([0, 1, 2, 3, 4, 5], 'A')
([0, 1, 2, 3, 5, 4], 'B')    ([0, 1, 3, 2, 5, 4], 'A')
([0, 1, 2, 4, 3, 5], 'C')    ([0, 1, 4, 5, 2, 3], 'A')
([0, 1, 2, 4, 5, 3], 'D')    ([0, 1, 5, 4, 3, 2], 'A')
([0, 1, 2, 5, 3, 4], 'E')    ([0, 2, 1, 4, 3, 5], 'A')
([0, 1, 2, 5, 4, 3], 'F')    ([0, 2, 3, 5, 1, 4], 'A')
([0, 1, 3, 2, 4, 5], 'E')    ([0, 2, 4, 1, 5, 3], 'A')
([0, 1, 3, 2, 5, 4], 'A')    ([0, 2, 5, 3, 4, 1], 'A')
([0, 1, 3, 4, 2, 5], 'B')    ([0, 3, 1, 5, 2, 4], 'A')
([0, 1, 3, 4, 5, 2], 'F')    ([0, 3, 2, 4, 5, 1], 'A')
([0, 1, 3, 5, 2, 4], 'C')    ([0, 3, 4, 2, 1, 5], 'A')
([0, 1, 3, 5, 4, 2], 'D')    ([0, 3, 5, 4, 1, 2], 'A')
([0, 1, 4, 2, 3, 5], 'D')    ([0, 4, 1, 3, 5, 2], 'A')
([0, 1, 4, 2, 5, 3], 'C')    ([0, 4, 2, 5, 1, 3], 'A')
([0, 1, 4, 3, 2, 5], 'F')    ([0, 4, 3, 1, 2, 5], 'A')
([0, 1, 4, 3, 5, 2], 'B')    ([0, 4, 5, 3, 2, 1], 'A')
([0, 1, 4, 5, 2, 3], 'A')    ([0, 5, 1, 2, 4, 3], 'A')
([0, 1, 4, 5, 3, 2], 'E')    ([0, 5, 2, 1, 3, 4], 'A')
([0, 1, 5, 2, 3, 4], 'D')    ([0, 5, 3, 1, 4, 2], 'A')
([0, 1, 5, 2, 4, 3], 'B')    ([0, 5, 4, 2, 3, 1], 'A')
([0, 1, 5, 3, 2, 4], 'F')    ([0, 1, 2, 3, 5, 4], 'B')
([0, 1, 5, 3, 4, 2], 'C')    ([0, 1, 3, 4, 2, 5], 'B')
([0, 1, 5, 4, 2, 3], 'E')    ([0, 1, 4, 3, 5, 2], 'B')
([0, 1, 5, 4, 3, 2], 'A')    ([0, 1, 5, 2, 4, 3], 'B')
([0, 2, 1, 3, 4, 5], 'D')    ([0, 2, 1, 5, 3, 4], 'B')
([0, 2, 1, 3, 5, 4], 'E')    ([0, 2, 3, 4, 1, 5], 'B')
([0, 2, 1, 4, 3, 5], 'A')    ([0, 2, 4, 5, 1, 3], 'B')
([0, 2, 1, 4, 5, 3], 'F')    ([0, 2, 5, 4, 3, 1], 'B')
([0, 2, 1, 5, 3, 4], 'B')    ([0, 3, 1, 5, 4, 2], 'B')
([0, 2, 1, 5, 4, 3], 'C')    ([0, 3, 2, 1, 4, 5], 'B')
([0, 2, 3, 1, 4, 5], 'C')    ([0, 3, 4, 5, 2, 1], 'B')
([0, 2, 3, 1, 5, 4], 'D')    ([0, 3, 5, 1, 2, 4], 'B')
([0, 2, 3, 4, 1, 5], 'B')    ([0, 4, 1, 2, 5, 3], 'B')
([0, 2, 3, 4, 5, 1], 'E')    ([0, 4, 2, 1, 3, 5], 'B')
([0, 2, 3, 5, 1, 4], 'A')    ([0, 4, 3, 2, 5, 1], 'B')
([0, 2, 3, 5, 4, 1], 'F')    ([0, 4, 5, 3, 1, 2], 'B')
([0, 2, 4, 1, 3, 5], 'F')    ([0, 5, 1, 4, 2, 3], 'B')
([0, 2, 4, 1, 5, 3], 'A')    ([0, 5, 2, 3, 1, 4], 'B')
([0, 2, 4, 3, 1, 5], 'E')    ([0, 5, 3, 2, 4, 1], 'B')
([0, 2, 4, 3, 5, 1], 'D')    ([0, 5, 4, 1, 3, 2], 'B')
([0, 2, 4, 5, 1, 3], 'B')    ([0, 1, 2, 4, 3, 5], 'C')
([0, 2, 4, 5, 3, 1], 'C')    ([0, 1, 3, 5, 2, 4], 'C')
([0, 2, 5, 1, 3, 4], 'C')    ([0, 1, 4, 2, 5, 3], 'C')
([0, 2, 5, 1, 4, 3], 'E')    ([0, 1, 5, 3, 4, 2], 'C')
([0, 2, 5, 3, 1, 4], 'F')    ([0, 2, 1, 5, 4, 3], 'C')
([0, 2, 5, 3, 4, 1], 'A')    ([0, 2, 3, 1, 4, 5], 'C')
([0, 2, 5, 4, 1, 3], 'D')    ([0, 2, 4, 5, 3, 1], 'C')
([0, 2, 5, 4, 3, 1], 'B')    ([0, 2, 5, 1, 3, 4], 'C')
([0, 3, 1, 2, 4, 5], 'F')    ([0, 3, 1, 2, 5, 4], 'C')
([0, 3, 1, 2, 5, 4], 'C')    ([0, 3, 2, 4, 1, 5], 'C')
([0, 3, 1, 4, 2, 5], 'E')    ([0, 3, 4, 5, 1, 2], 'C')
([0, 3, 1, 4, 5, 2], 'D')    ([0, 3, 5, 4, 2, 1], 'C')
([0, 3, 1, 5, 2, 4], 'A')    ([0, 4, 1, 3, 2, 5], 'C')
([0, 3, 1, 5, 4, 2], 'B')    ([0, 4, 2, 3, 5, 1], 'C')
([0, 3, 2, 1, 4, 5], 'B')    ([0, 4, 3, 1, 5, 2], 'C')
([0, 3, 2, 1, 5, 4], 'F')    ([0, 4, 5, 2, 1, 3], 'C')
([0, 3, 2, 4, 1, 5], 'C')    ([0, 5, 1, 4, 3, 2], 'C')
([0, 3, 2, 4, 5, 1], 'A')    ([0, 5, 2, 3, 4, 1], 'C')
([0, 3, 2, 5, 1, 4], 'D')    ([0, 5, 3, 2, 1, 4], 'C')
([0, 3, 2, 5, 4, 1], 'E')    ([0, 5, 4, 1, 2, 3], 'C')
([0, 3, 4, 1, 2, 5], 'D')    ([0, 1, 2, 4, 5, 3], 'D')
([0, 3, 4, 1, 5, 2], 'E')    ([0, 1, 3, 5, 4, 2], 'D')
([0, 3, 4, 2, 1, 5], 'A')    ([0, 1, 4, 2, 3, 5], 'D')
([0, 3, 4, 2, 5, 1], 'F')    ([0, 1, 5, 2, 3, 4], 'D')
([0, 3, 4, 5, 1, 2], 'C')    ([0, 2, 1, 3, 4, 5], 'D')
([0, 3, 4, 5, 2, 1], 'B')    ([0, 2, 3, 1, 5, 4], 'D')
([0, 3, 5, 1, 2, 4], 'B')    ([0, 2, 4, 3, 5, 1], 'D')
([0, 3, 5, 1, 4, 2], 'F')    ([0, 2, 5, 4, 1, 3], 'D')
([0, 3, 5, 2, 1, 4], 'E')    ([0, 3, 1, 4, 5, 2], 'D')
([0, 3, 5, 2, 4, 1], 'D')    ([0, 3, 2, 5, 1, 4], 'D')
([0, 3, 5, 4, 1, 2], 'A')    ([0, 3, 4, 1, 2, 5], 'D')
([0, 3, 5, 4, 2, 1], 'C')    ([0, 3, 5, 2, 4, 1], 'D')
([0, 4, 1, 2, 3, 5], 'E')    ([0, 4, 1, 5, 3, 2], 'D')
([0, 4, 1, 2, 5, 3], 'B')    ([0, 4, 2, 5, 3, 1], 'D')
([0, 4, 1, 3, 2, 5], 'C')    ([0, 4, 3, 2, 1, 5], 'D')
([0, 4, 1, 3, 5, 2], 'A')    ([0, 4, 5, 1, 2, 3], 'D')
([0, 4, 1, 5, 2, 3], 'F')    ([0, 5, 1, 3, 2, 4], 'D')
([0, 4, 1, 5, 3, 2], 'D')    ([0, 5, 2, 1, 4, 3], 'D')
([0, 4, 2, 1, 3, 5], 'B')    ([0, 5, 3, 4, 2, 1], 'D')
([0, 4, 2, 1, 5, 3], 'E')    ([0, 5, 4, 3, 1, 2], 'D')
([0, 4, 2, 3, 1, 5], 'F')    ([0, 1, 2, 5, 3, 4], 'E')
([0, 4, 2, 3, 5, 1], 'C')    ([0, 1, 3, 2, 4, 5], 'E')
([0, 4, 2, 5, 1, 3], 'A')    ([0, 1, 4, 5, 3, 2], 'E')
([0, 4, 2, 5, 3, 1], 'D')    ([0, 1, 5, 4, 2, 3], 'E')
([0, 4, 3, 1, 2, 5], 'A')    ([0, 2, 1, 3, 5, 4], 'E')
([0, 4, 3, 1, 5, 2], 'C')    ([0, 2, 3, 4, 5, 1], 'E')
([0, 4, 3, 2, 1, 5], 'D')    ([0, 2, 4, 3, 1, 5], 'E')
([0, 4, 3, 2, 5, 1], 'B')    ([0, 2, 5, 1, 4, 3], 'E')
([0, 4, 3, 5, 1, 2], 'E')    ([0, 3, 1, 4, 2, 5], 'E')
([0, 4, 3, 5, 2, 1], 'F')    ([0, 3, 2, 5, 4, 1], 'E')
([0, 4, 5, 1, 2, 3], 'D')    ([0, 3, 4, 1, 5, 2], 'E')
([0, 4, 5, 1, 3, 2], 'F')    ([0, 3, 5, 2, 1, 4], 'E')
([0, 4, 5, 2, 1, 3], 'C')    ([0, 4, 1, 2, 3, 5], 'E')
([0, 4, 5, 2, 3, 1], 'E')    ([0, 4, 2, 1, 5, 3], 'E')
([0, 4, 5, 3, 1, 2], 'B')    ([0, 4, 3, 5, 1, 2], 'E')
([0, 4, 5, 3, 2, 1], 'A')    ([0, 4, 5, 2, 3, 1], 'E')
([0, 5, 1, 2, 3, 4], 'F')    ([0, 5, 1, 3, 4, 2], 'E')
([0, 5, 1, 2, 4, 3], 'A')    ([0, 5, 2, 4, 1, 3], 'E')
([0, 5, 1, 3, 2, 4], 'D')    ([0, 5, 3, 1, 2, 4], 'E')
([0, 5, 1, 3, 4, 2], 'E')    ([0, 5, 4, 3, 2, 1], 'E')
([0, 5, 1, 4, 2, 3], 'B')    ([0, 1, 2, 5, 4, 3], 'F')
([0, 5, 1, 4, 3, 2], 'C')    ([0, 1, 3, 4, 5, 2], 'F')
([0, 5, 2, 1, 3, 4], 'A')    ([0, 1, 4, 3, 2, 5], 'F')
([0, 5, 2, 1, 4, 3], 'D')    ([0, 1, 5, 3, 2, 4], 'F')
([0, 5, 2, 3, 1, 4], 'B')    ([0, 2, 1, 4, 5, 3], 'F')
([0, 5, 2, 3, 4, 1], 'C')    ([0, 2, 3, 5, 4, 1], 'F')
([0, 5, 2, 4, 1, 3], 'E')    ([0, 2, 4, 1, 3, 5], 'F')
([0, 5, 2, 4, 3, 1], 'F')    ([0, 2, 5, 3, 1, 4], 'F')
([0, 5, 3, 1, 2, 4], 'E')    ([0, 3, 1, 2, 4, 5], 'F')
([0, 5, 3, 1, 4, 2], 'A')    ([0, 3, 2, 1, 5, 4], 'F')
([0, 5, 3, 2, 1, 4], 'C')    ([0, 3, 4, 2, 5, 1], 'F')
([0, 5, 3, 2, 4, 1], 'B')    ([0, 3, 5, 1, 4, 2], 'F')
([0, 5, 3, 4, 1, 2], 'F')    ([0, 4, 1, 5, 2, 3], 'F')
([0, 5, 3, 4, 2, 1], 'D')    ([0, 4, 2, 3, 1, 5], 'F')
([0, 5, 4, 1, 2, 3], 'C')    ([0, 4, 3, 5, 2, 1], 'F')
([0, 5, 4, 1, 3, 2], 'B')    ([0, 4, 5, 1, 3, 2], 'F')
([0, 5, 4, 2, 1, 3], 'F')    ([0, 5, 1, 2, 3, 4], 'F')
([0, 5, 4, 2, 3, 1], 'A')    ([0, 5, 2, 4, 3, 1], 'F')
([0, 5, 4, 3, 1, 2], 'D')    ([0, 5, 3, 4, 1, 2], 'F')
([0, 5, 4, 3, 2, 1], 'E')    ([0, 5, 4, 2, 1, 3], 'F')

I don't completely understand how you did this yet, but I will dig into the results you've shared here soon! Thank you so much for taking the time to do this. I really appreciate it!! — Ginseng English, Mar 31 '20 at 19:38
@Rob Brute force exhaustive search: Assume first $n$ hexagons are labeled "correctly". To label $(n+1)$th hexagon, look at all of its subsequences and make a list of labels $L_n$ that have already been used for those subsequences in previous $n$ labeled hexagons. To label it "correctly", we must use a label that is not in $L_n$. If we have multiple choices for a label, we "branch out" into each of those possibilities. If $L_n={A,B,C,D,E,F}$ we can't pick a new label and current "branch" can't lead to a solution, so we go back and try another "branch". $-$I wrote a python program to do this. — Vepir, Mar 31 '20 at 20:00
Thank you so much for this. I finally had a chance to sit down with this and understand how it works and it's brilliant. Maybe for you it was simple, but I was approaching this problem from the exact wrong way, trying to match the letters to the 5-digit sequences, when what really mattered was just distributing out the subsequences. — Ginseng English, Apr 04 '20 at 12:50
@ben10 I'm sorry! I'm not a programmer, so when you asked about an "exhaustive search" I didn't understand that this was a technical term with a precise meaning. — Ginseng English, Apr 04 '20 at 12:51
Okay, so I hope I'm not pushing my luck here, but I actually have a second question that I had given up hope on. Now that I see how elegantly (and perhaps simply?) you solved my last one, I wonder if this other one is feasible after all: — Ginseng English, Apr 04 '20 at 12:54
Any two-digit subsequence occurs exactly 24 times. Is there a way to distribute the letters to the 5-digit sequences such that each letter aligns with each 3-digit subsequence exactly once (as above) and each 2-digit subsequence exactly 4 times? — Ginseng English, Apr 04 '20 at 13:02
@Rob "Exhaustive search" simply means to check all possibilities. In the "Brute force exhaustive search: ..." process I described in my previous comment, I go only over "correctly labeled" possibilities to make my search reasonable (and use "recursion" when I describe the "branches"). This is still not necessarily the best way to solve such a problem. One alternative I currently see is to perhaps translate the problem into graph theory where it becomes a coloring problem. — Vepir, Apr 04 '20 at 13:20
@Rob I think the above solution does have the property that "each letter aligns with each 2-digit subsequence exactly 4 times". I've ran a quick check now and this should be true. — Vepir, Apr 04 '20 at 13:43

Distributing Series/Patterns

1 Answers1