The integral $$ \int_0^\infty \frac{\sin x\sinh x}{\cos (2 x)+\cosh \left(2x \right)}\frac{dx}{x}=\frac{\pi}{8}, $$ is given as equation $(17)$ in M.L. Glasser, Some integrals of the Dedekind $\eta$-function.
More general integral $$ \int_0^\infty \frac{\sin x\sinh (x/a)}{\cos (2 x)+\cosh \left(2x/a\right)}\frac{dx}{x}=\frac{\tan^{-1} a}{2},\tag{1} $$ can be deduced as a limiting case of formula $4.123.6$ in Gradsteyn and Ryzhik.
I have been looking for finite elementary analogs of integral $(1)$ and have proved that \begin{align}\label{} \int_0^{1}\frac{\sin \bigl(n \sin^{-1}t\bigr)\sinh \bigl(n \sinh^{-1}(t/a)\bigr)}{\cos \bigl( 2 n \sin^{-1}t\bigr)+\cosh \bigl(2 n \sinh^{-1}(t/a)\bigr)}\frac{dt}{t \sqrt{1-t^2} \sqrt{1+{t^2}/{a^2}}}=\frac{\tan^{-1} a}{2},\tag{1a} \end{align} for an odd integer $n$.
When $n\to\infty$ equation $(1a)$ will give equation $(1)$. This is easy to see because when $n$ is large then the main contribution to $(1a)$ comes from a small neighborhood around $0$.
Q: Can you explain why this integral has such a simple closed form and in particular why it has the same value for all odd $n$?
I want to stress that I have a proof which is based on partial fractions expansion for odd $n$ \begin{align} &\frac{\sin \bigl(n \sin^{-1}t\bigr)\sinh \bigl(n \sinh^{-1}(t/a)\bigr)}{\cos \bigl( 2 n \sin^{-1}t\bigr)+\cosh \bigl(2 n \sinh^{-1}(t/a)\bigr)}\frac{2n}{t^2}\\&=\sum _{j=1}^n\frac{i(-1)^{j-1} }{\sin\frac{\pi (2 j-1)}{2 n}}\cdot \frac{\left(a\cos\frac{\pi (2 j-1)}{2 n}+i\right) \left(a+i \cos\frac{\pi (2 j-1)}{2 n}\right)}{t^2 \left(a^2-1+2 ia \cos\frac{\pi (2 j-1)}{2 n}\right)-a^2 \sin ^2\frac{\pi (2 j-1)}{2 n}}, \end{align} the elementary integral \begin{align} \int_0^1 \frac{t}{t^2 \left(a^2-1+2 ia \cos\frac{\pi (2 j-1)}{2 n}\right)-a^2 \sin ^2\frac{\pi (2 j-1)}{2 n}}\frac{dt}{\sqrt{1-t^2} \sqrt{1+{t^2}/{a^2}}}\\=\frac{\tan^{-1}a+i\tanh^{-1}\cos\frac{\pi (2 j-1)}{2 n}}{i\left(a\cos\frac{\pi (2 j-1)}{2 n}+i\right) \left(a+i \cos\frac{\pi (2 j-1)}{2 n}\right)}, \end{align} and summation formula which can be deduced from the partial fractions above $$ \sum _{j=1}^n \frac{(-1)^{j-1}}{\sin \frac{\pi (2 j-1)}{2 n}}=n. $$
Details can be found here https://arxiv.org/abs/2008.04097
But despite this prove I don't understand why all these cancellations occur to give such a simple result at the end. I suspect there is a very short and transparent proof which explains why the integral is $\frac{\tan^{-1} a}{2}$ for all odd $n$. Maybe Glasser's master theorem or some contour integration can explain this formula? Motivation for this question is desire to understand this integration formula.
Any alternative proof is welcome if it is not just a detailed version of the proof above. Any ideas and comments are welcome. Thanks.
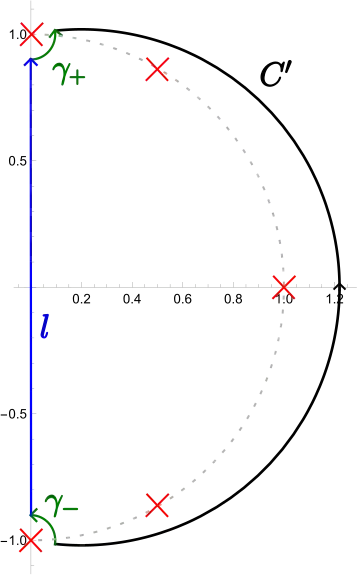 $w$ plane" />
$w$ plane" />