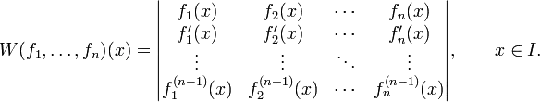6

I want to find some $m \times n$ (where $m>n$) matrices that have the property that any submatrix with $n$ rows has full rank. The Vandermonde and Cauchy matrices are the only two matrices I know. Can you please give me some other matrices?

P.S. I forgot to mention that the entries in the matrices must be integers, and the base field is infinite field.

Rodrigo de Azevedo
  • 23,223
foool
  • 247
  • 1
    What is the base field? – azimut Apr 12 '13 at 13:25
  • @azimut, Will the base field influences the result? as far as I know, a vandermonde matrix has a full rank in a finite field as well as in a infinite field. – foool Apr 13 '13 at 00:27
  • Over a finite field, there are only finitely many different row vectors of length $n$. Hence the matrix you require does not exist when $m$ is large enough. – user1551 Apr 13 '13 at 04:43
  • @user1551 You are right. When $m$ is less than the field size, the matrix can not be found. But if the $m$ is large, entries can be get from a larger finite field. So for simplicity, I change the base field to the infinite field and I guess it doesn't affect the result. – foool Apr 13 '13 at 07:26
  • With $m=n+1$, an $n\times n$ identity matrix with a row of all $1$'s. For that matter, any invertible $n\times n$ matrix, appended by a row that is a linear combination of the first $n$ rows using weights that are all nonzero. – 2'5 9'2 Apr 26 '13 at 02:44
  • @alex.jordan Thanks, but you just give me an example of the vandermonde matrix. – foool Apr 26 '13 at 07:32
  • @foool Just to check my memory was functioning, I looked up Vandermonde matrix and that example is not a standard VM. Its a "confluent VM", something I'd not heard of. – 2'5 9'2 Apr 28 '13 at 05:15

2 Answers2

1

Let the entries be $\sqrt{p_i}$ for distinct primes $p_i$.

EDIT: It appears the entries are to be integers. If you take them to be distinct members of a sufficiently rapidly growing sequence, maybe $10^{10^{k!}}$ for $1\le k\le mn$, then no $n\times n$ submatrix can be singular. For any such matrix will have an entry much bigger than all the others, so if you evaluate the determinant by expanding along the row or column containing that entry, the coefficient of that entry would have to be zero for the determinant to vanish; but that coefficient is an $n-1\times n-1$ determinant, and induction takes over.

Gerry Myerson
  • 185,413
  • Please explain why. It's not obvious to me, at least. – vonbrand Apr 12 '13 at 13:42
  • Consider an $n\times n$ submatrix. Compute its determinant by expanding along the first row. You get a linear combination of the entries of the first row being zero, but the elements in the first row are linearly independent over the field generated by the other entries, so all the coefficients must be zero. The coefficients are order $n-1$ determinants, so we win by induction on $n$. – Gerry Myerson Apr 12 '13 at 13:54
  • @GerryMyerson the entries are integers, sorry I didn't mention before. I guess if the entries are distinct irrational numbers, the matrix has a full rank, and you just provide a method to generate them, am I right? – foool Apr 13 '13 at 00:49
  • Distinct irrationals doesn't imply full rank, e.g., $$\pmatrix{\sqrt6&\sqrt{12}\cr\sqrt5&\sqrt{10}\cr}$$ If you mean for the entries to be integers, please edit that into your question. But if the entries are integers, then they are not in a finite field. Maybe you should think about what exactly it is that you want to ask. – Gerry Myerson Apr 13 '13 at 06:05
  • @GerryMyerson You are right, Distinct irrationals doesn't imply full rank. I know what exactly what I want to ask, maybe I didn't say it clearly. Whether the base field is a finite field or infinite field doesn't affect the result, so let's forget about it. But entries must be integers and I edit the question. – foool Apr 13 '13 at 07:32
  • It doesn't make any sense to say the base field is finite and the entries are integers. – Gerry Myerson Apr 13 '13 at 11:33
  • @GerryMyerson I mean these integers are just symbols that represent elements in a finite field, not common integers in the infinite field. – foool Apr 13 '13 at 12:32
0

The Moore Matrix is similar to vandermonde matrix and has a full rank, but it is more generalized.

Moore Matrix

The Wronskian determinant can be used to generate full-rank matrices.

enter image description here

foool
  • 247
  • If we restrict the entries are from finite field, is it still possible to apply the Wronskian determinant to generate full-rank matrices? – Idonknow Sep 14 '14 at 15:37
  • @Idonknow Thanks for you mention! Frankly, I don't know whether the Wronskian determinant can be used to generate full matrices or not, but the Moore matrix and Wronskian determinant is as far as I can get, so if you have any better idea or more information about the Wronskian determinant applying in a field, please let me know. Many thanks. – foool Sep 22 '14 at 13:56