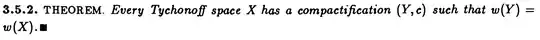Every Tychonoff space $X$ has a compactification $(Y,c)$ such that the weight of $X$ is the same of $Y$.

Question

Following a reference from "General Topology" by Ryszard Engelking

First of all I ask a proof of the statement and then I ask if every Tychonoff space $X$ have a Hausdorff compactification $(Y,c)$ such the weight of $X$ is the same of $Y$.

As reference I say that the weight $w(X)$ of a topological space $X$ is the following quantity:

$$ w(X)=\min\{|\mathcal{B}|:\mathcal{B}\text{ is a base for } X \} + \aleph_0 $$

Could someone help me, please?

You should give some more context. What is the weight of a space? — Keen-ameteur, Mar 23 '20 at 17:31

score 2 · Accepted Answer · answered Mar 23 '20 at 22:33

2

By the Ursyohn embedding theorem, if $\kappa=w(X)$, we can embed $X$ into $[0,1]^\kappa$ (in the product topology) via some embedding $e: X \to [0,1]^\kappa$, this uses that $X$ is a Tychonoff space.

Then $Y=\overline{e[X]}$ and $c =e$ is the required compactification, as all subspaces of $[0,1]^\kappa$ have weight $\le \kappa$ and $Y$ is compact Hausdorff as a closed subspace of the compact (Tychonoff!) Hausdorff cube $[0,1]^\kappa$.

answered Mar 23 '20 at 22:33

Henno Brandsma

250,824

Okay, but why $w(Y)\le k:=w(X)$? – Antonio Maria Di Mauro Mar 23 '20 at 22:42
1

$w(X) = w(e[X]) \le w(Y)$ as $e[X] \subseteq Y$ and so $\kappa =w(X) \le w(Y) \le \kappa$ hence equality. – Henno Brandsma Mar 23 '20 at 22:50
Sorry, I didn't explain myself well: I don't understand why if $Y\subseteq[0,1]^k$ then $w(Y)\le k$. – Antonio Maria Di Mauro Mar 23 '20 at 22:51
1

@AntonioMariaDiMauro Because $w([0,1]^\kappa)=\kappa$ for all infinite cardinals $\kappa$, and subspaces have weight $\le \kappa$ because of that. – Henno Brandsma Mar 23 '20 at 22:53
Okay, unfortunately I didn't know it; so how to prove it? – Antonio Maria Di Mauro Mar 23 '20 at 22:54
@AntonioMariaDiMauro earlier theorem in Engelking. You're quoting from the middle of his text... – Henno Brandsma Mar 23 '20 at 22:55
Okay, so I am looking in Engelking. – Antonio Maria Di Mauro Mar 23 '20 at 22:56
@AntonioMariaDiMauro I give the essential argument for another cube $D(\kappa)^\kappa$ here as well. – Henno Brandsma Mar 23 '20 at 22:58
1

To the proposer: If $B$ is a base for $X$ with $|B|\le k,$ and if $Y\subset X$ then $B'= {b\cap Y:b\in B}$ is base for $Y$ with $|B'|\le k.$ – DanielWainfleet Mar 24 '20 at 06:41
@HennoBrandsma Naturally the compactification is $T_2$ since $[0,1]^k$ is $T_2$ and so too $Y$, right? – Antonio Maria Di Mauro Mar 25 '20 at 15:14
@AntonioMariaDiMauro yep. – Henno Brandsma Mar 25 '20 at 15:20

Every Tychonoff space $X$ has a compactification $(Y,c)$ such that the weight of $X$ is the same of $Y$.

1 Answers1