Problem about differential of a linear map

Question

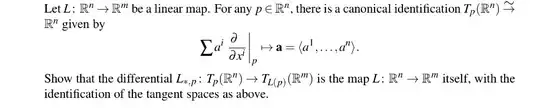
Please can you tell how to solve this problem clearly? Please solve this explanatorily. Thank you

Answer 1

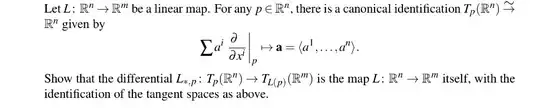
Say that $F: N^n \to M^m$ is a smooth function, mapping $$ p = \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \mapsto \begin{bmatrix} y_1 \\ \vdots \\ y_m \end{bmatrix} = \begin{bmatrix} F_1(p) \\ \vdots \\ F_m(p) \end{bmatrix} = F(p). $$

Then, the differential is linear map $F_{*,p}: T_p(N) \to T_{F(p)}(M)$ between the tangent spaces. Choosing the basis $\{ \frac{\partial}{\partial x_1}, \dots, \frac{\partial}{\partial x_n} \}$ for $T_p(N)$ and the basis $\{ \frac{\partial}{\partial y_1}, \dots, \frac{\partial}{\partial y_m} \}$ for $T_{F(p)}(M)$, we can represent the differential by the $(m \times n)$-matrix $$ \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \frac{\partial F_1(x)}{\partial x_1} & \cdots & \frac{\partial F_1(x)}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial F_m(x)}{\partial x_1} & \cdots & \frac{\partial F_m(x)}{\partial x_n} \end{bmatrix} $$ In the special case that $L: \mathbb{R}^n \to \mathbb{R}^m$ is a linear map, we can write $L(x) = Ax$, where $A$ is an $(m \times n)$-matrix.

What do the partial derivatives look like? Put $A = [a_{ij}]$, so for any $1 \le i \le m$, $$ y_i = F_i(x) = a_{i1}x_1 + \cdots + a_{in}x_n, $$ and for any $1 \le i \le m$, $1 \le j \le n$, $$ \frac{\partial F_i(x)}{\partial x_j} = \frac{\partial}{\partial x_j}\big( a_{i1}x_1 + \cdots + a_{in}x_n \big) = a_{ij}. $$

Thus, the matrix of partial derivatives, representing the differential of $L$ in coordinates, is nothing other than the matrix of $L$ itself, once we make the identification $T_p(\mathbb{R}^n) \overset{\sim}{\to} \mathbb{R}^n$.