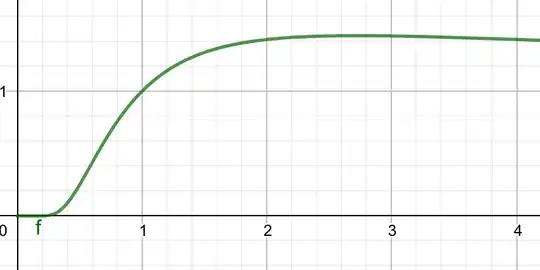
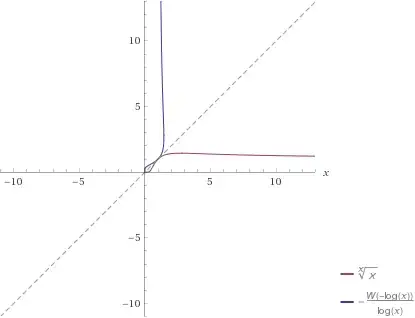
Let us consider a function:
$f(x)= x^{x^{x^\cdots}}$
what will be the domain of this function.
Like $f(1)=1$, $f(\sqrt2)=2$, but $f(2)$ will reach out to infinity. So, what is the domain of $f(x)$ Edit:- Will it also contains negative numbers if we include complex numbers?
If $f(x)=x^{x^{x^\cdots}}$ is equal to a real number $y$, then it would follow that $y=x^y$. Then, $$\log_y(y)=\log_y(x^y)$$ $$1=y\log_y(x)$$ $$\frac1y=\log_y(x)$$ $$x=y^\frac1y$$
Therefore $f(x)$ is the inverse of $y=x^\frac1x$. Now, look at the graph of $x^\frac1x$:
As you can see, $0\leq x^\frac1x$ and $x^\frac1x$ has a maximum somewhere between $x=2$ and $x=3$. (You can use differentiation to show that the global maximum is $x=e$). Therefore, $f(x)$ has a range of $[0,e^\frac1e]$, as this graph shows:
