3

This question is about part (a) of this proposition:

enter image description here

Here is a plan of the proof.

enter image description here

Here's what the picture looks like, from what I understand:

enter image description here

But I don't understand what the condition $s\circ p=t\circ p$ means. I guess this means componentwise equality: $s_u\circ p_u=t_u\circ p_u $ for all $u$, but what is $p_u$? $L$ is not a product, and so $p_u$ cannot be a projection.

I'm just trying to prove first that $Du\circ p_I=p_J$ for all $u: I\to J$, and it seems I need to use $s\circ p=t\circ p$ to that end, which is unclear how to do.

user557
  • 12,359
  • There is a typo on the picture: $t_u=pr_J$ should be replaced by $t_u=pr_K$. – user557 Feb 19 '20 at 02:13
  • Thanks for the link in the first sentence and this post, it is helping me greatly understand "Pullbacks & terminal object imlplies has all finite limits". – Daniel Donnelly Dec 20 '21 at 17:49

2 Answers2

3

$s \circ p = t \circ p$ are both arrows into a product, the equality here is equivalent to them being equal after each projection, i.e., $\pi_u \circ s \circ p = \pi_u \circ t \circ p$ for all $u : J \to K$ in $\mathbf I$.

Now, $\pi_u \circ s$ is the $u$-component of $s$, hence is equal to $D(u) \circ \text{pr}_J$. Similarly, $\pi_u \circ t = \text{pr}_K$. Combining this with the previous equality, we find $D(u) \circ \text{pr}_J \circ p = \text{pr}_K \circ p$. Now, by definition $p_I = \text{pr}_I \circ p$ for any $I \in \mathbf I$ (i.e. $p_I$ is the $I$-component of $p$), we find $D(u) \circ p_J = p_K$.

Hence $(L, (p_I : L \to D(I))_{I \in \mathbf I})$ is a cone. Hopefully this clears up the confusion.

Rushy
  • 1,502
  • 9
  • 11
  • Where does the statement "the equality here is equivalent to them being equal after each projection" come from? Is it some definition? If so, the definition of what? – user557 Feb 19 '20 at 00:29
  • And regarding $p_I$, I thought from the text of the exercise that $p_I$ is something that you should get "automatically" from $p$. However, you did not say "we have this $p$, so by definition $p_I$ are given by such and such formula"; instead you "adjusted" the definition of $p_I$ so that $(L, p_I)$ becomes a cone. So is there a definition that would immediately give the formula for $p_I$ that you obtained?

    Addition: In other words, what I mean is that Leinster writes "write $p_I$ for the $I$th component of $p$". So there must be some general definition of the $I$th component of $p$.

     – user557 Feb 19 '20 at 00:33
  • 1
    The equivalence follows from the universal property of the product. Certainly if two arrows into a product are equal, they are equal after the projections. Conversely, if they are equal after each projection, you have two morphisms that make the same product diagram commute, hence by uniqueness they must be equal. – Rushy Feb 19 '20 at 00:38
  • 1
    For $p_I$, for an arrow $p$ into a product, indexed by some index set $\mathbf I$, the $I$-component of $p$ generally refers to $p$ followed by the projection onto the corresponding factor. This is also how $s$ and $t$ are defined, by defining their components and then using the universal property. – Rushy Feb 19 '20 at 00:41
  • So you could have started by saying that by definition, $p_I=pr_I\circ p$, and then verified that $D(u)\circ p_J=p_K$? – user557 Feb 19 '20 at 00:45
  • Yes, Leinster has a definition for it in the section on the product (slighty after definition 5.1.7). – Rushy Feb 19 '20 at 00:49
  • I'm not sure I understand why what Leinster has after def. 5.1.7 is related to our $p$. Leinster says that if there is a limit cone $(P,p_i)$ and a secondary cone $(A,f_i)$, then the $i$th component of the unique map $A\to P$ is $f_i$. But in our case we don't have any secondary cone, we only have "a vertex" $A=L$ and a map $L\to P=\prod D(I)$. That is, we only have the first element of the pair $(A, f_i)$, viz. $A=L$, but not the second element ($f_i$). – user557 Feb 19 '20 at 00:58
  • Probably $f_i$ arise automatically as $pr_i\circ p$, in which case the definition applies. Anyway, the idea is clear. – user557 Feb 19 '20 at 01:00
  • $p$ is not an arrow between cones, but an arrow into a product, and we use its components to get the cone for the diagram. – Rushy Feb 19 '20 at 01:05
  • I suppose the misunderstanding is because P, together with its projections does not necessarily form a cone. $D(u) \circ pr_J$ is not necessarily equal to $pr_K$. – Rushy Feb 19 '20 at 01:15
  • Is it true that if $(L', f_I){I\in\mathbf I}$ is a cone, then there exists an arrow $f: L'\to \prod{I\in\mathbf I} D(I)$ such that the $I$th component of $f$ is $f_I$? It seems that this is needed to finish the proof. – user557 Feb 19 '20 at 01:21
  • 1
    Yes, this is the universal property of the product. In fact, for any set of morphisms $f_I : L' \to D(I)$ there exists such an arrow, cone or not. – Rushy Feb 19 '20 at 01:31
  • By cone here I mean cone on the diagram $D$ by the way. The product is technically a limiting cone, but not for the diagram being considered, however this would probably be a bit ambiguous. If you'd like, I can update the answer to be more complete and express everything in terms of their appropriate cones, but that will have to wait until tomorrow – Rushy Feb 19 '20 at 01:45
  • After the mention of Leinster's definition, I got a little lost in what you are trying to say. I think I got the main idea, but I may be missing something without realizing it. If you are willing to write more on what you mean, I'd be of course glad to read it, but if you don't have time, it's fine too. I also posted an answer with the second part of the proof. – user557 Feb 19 '20 at 02:00
  • By definition, $t\circ p$ is a family of maps $(\pi_u\circ t\circ p)$ where each element of the family is the $u$th component of $t\circ p$. Can we define two such maps to be equal if their components are equal (instead of using the universal property of the product)? – user557 Feb 19 '20 at 03:08
  • You could, but it is a direct consequence of the properties of the product that two arrows $a : Z \to \prod_{i \in I} X_i$, $b : Z \to \prod_{i \in I} X_i$ are equal if and only if $p_i \circ a = p_i \circ b$ for all $i \in I$, where $p_i : \prod_{j \in I} X_j \to X_i$ is the projection, so it doesn't really change anything – Rushy Feb 19 '20 at 15:23
2

This is the second part of the proof (the first part is Rushy's answer).

We need to show that if $(L', f_I:L'\to D(I))_{I\in\mathbf{I}}$ is another cone, then there exists a unique arrow $\alpha: L'\to L$ such that $p_J\circ\alpha=f_J$ for all $J\in\mathbf I$.

So let $(L', f_I:L'\to D(I))_{I\in\mathbf{I}}$ be a cone. By the universal property of the product, there exists a unique arrow $f: L'\to \prod_{I\in\mathbf I} D(I)$ such that $pr_J\circ f=f_I$. (In other words, the $I$th component of $f$ is $f_I$.)

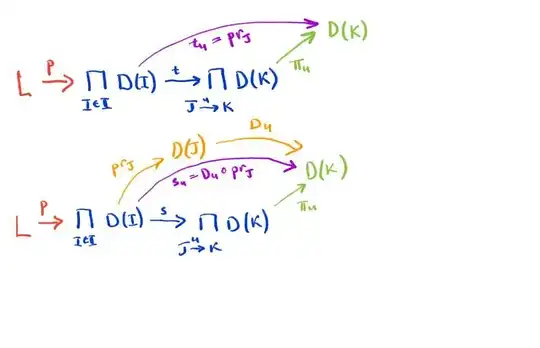
Note that $s\circ f=t\circ f$. Indeed,

$$s\circ f=t\circ f \\ \iff \pi_u\circ s\circ f=\pi_u\circ t \circ f \text{ (see Rushy's comment under the answer)}\\ \iff s_u\circ f=t_u\circ f \text{ (definition of the }u\text{th component of $s$ and $t$)} \\ \iff Du\circ pr_J\circ f =pr_K\circ f \text{ (definitions of $t_u$ and $s_u$)} \\ \iff Du\circ f_J=f_K \text{ (by the above)}$$ The equality in the last row holds because $(L', f_I:L'\to D(I))_{I\in\mathbf{I}}$ is a cone. Thus $s\circ f=t\circ f$.

Since $(L,p:L\to \prod_{I\in\mathbf I} D(I))$ is an equalizer of $s$ and $t$, there is a unique $\alpha: L'\to L$ such that $p\circ\alpha=f$. Again, by the answer in the comments, this is equivalent to $pr_J \circ p\circ \alpha=pr_J\circ f$. Since $pr_J\circ \alpha=p_J$ and $pr_J\circ f=f_J$, we can rewrite that as $p_J\circ \alpha=f_J$. That's what we needed to prove.

Rushy
  • 1,502
  • 9
  • 11
user557
  • 12,359