0

enter image description here

I have completed part(a) to find the $y$-Lipschitz constant $L=3$, I'm just not sure how to start part (b), determining a step size to guarantee a global error less than $10^{-3}$.

Any help would be greatly appreciated.

Thanks!

(after comments) I have followed the link and put my values into the formula $$|w_i-y_i|\le \frac{Mh}{2L}(e^{L(x_i-a)}-1)$$ with $w_i−y_i=0.001$, $M=40$, $L=3$ and $x_i−a=3−1=2$; but then when everything cancels out, I get $h=3.727\cdot 10^{-7}$. Any idea where I might be going wrong?

nmasanta
  • 9,640
DFielding96
  • 23
  • 2
    Dear @DFielding96, MSE is not meant to solve homeworks for you: you should post your attempts, some ideas you get for attack the problem, and explain where you are stucked, then other users will help you :) – qwertyguy Feb 17 '20 at 15:00
  • 1
    Yes, what did you get for part (a)? – mjw Feb 17 '20 at 16:19
  • 2
    It would be nice if you would transcribe the relevant part of the task using mathjax. Also write down the details of what you already know about the task and its solution and what you suspect is further applicable. The error bound to apply is explained for instance here, the second derivative is needed to compute $M$. – Lutz Lehmann Feb 17 '20 at 16:20
  • @mjw I got f(x,y) = 2-sin(xy) and L=3. I don't understand the wording of/u:
    You can assume that the exact solution fulfills |y''(x)| ≤ 40. Or what I need to do with that information     – DFielding96 Feb 17 '20 at 16:20
  • 3
    Please edit your post to add primary and additional information. Yes, $M$ is a bound on the second derivative of the exact solution. Adding some $ will format as math formula, using \ in function names will render them as function names, $f(x,y) = 2-\sin(xy)$ and $L=3$ => $f(x,y) = 2-\sin(xy)$ and $L=3$. – Lutz Lehmann Feb 17 '20 at 16:29
  • 1
    Imagine that the average visitor will not open your scan image, in the question lists only the first 3 lines or less will appear. Structure your question accordingly, primarily so that all necessary basic information about the task is available without the image. – Lutz Lehmann Feb 17 '20 at 16:52
  • @LutzLehmann I have followed the link above and put my values into the formula £$$|w_i-y_i|\le \frac{Mh}{2L}(e^{L(x_i-a)}-1)$$ with $w_i - y_i = 0.001$ , $M=40$ , $L=3$ and $x_i-a = 3-1 = 2$ but then when everything cancels out, I get $h=3.727x10^-7$ Any idea where I might be going wrong? – DFielding96 Feb 17 '20 at 17:42
  • Nothing is wrong, I get the same value from that theoretical bound. Note that the theoretical bound is in all steps of its derivation strictly pessimistic, in practice the contributions are not always maximum and some local errors my have opposite sign and thus partially cancel out. My answer contains an a-posteriory estimate of the error behavior, essentially extrapolated from 2 points, but still surprisingly accurate. // With some care one can show that $|y''(x)|\le15$, but that is only a factor of about $2$. – Lutz Lehmann Feb 17 '20 at 17:56
  • @LutzLehmann SO my answer for $h$ is correct? Seems strange for it to be so small, Does it all check out properly? – DFielding96 Feb 17 '20 at 17:59
  • Let us continue this discussion in chat. – DFielding96 Feb 17 '20 at 18:03
  • Yes, it is correct. In my experience it is the $L$ in the exponential that is about a factor $10$ or so too large (as factor in the exponent, not as Lipschitz constant) – Lutz Lehmann Feb 17 '20 at 18:03

1 Answers1

1

Solving the problem with 5 and 10 steps gives the table

x=1.40,  y_1= 0.49177, y_2= 0.69178,  c(1.4)=-1.00004
x=1.80,  y_1= 1.03763, y_2= 1.32076,  c(1.8)=-1.41567
x=2.20,  y_1= 1.45513, y_2= 2.03157,  c(2.2)=-2.88222
x=2.60,  y_1= 2.27899, y_2= 2.48297,  c(2.6)=-1.01988
x=3.00,  y_1= 3.21908, y_2= 3.81554,  c(3.0)=-2.98229

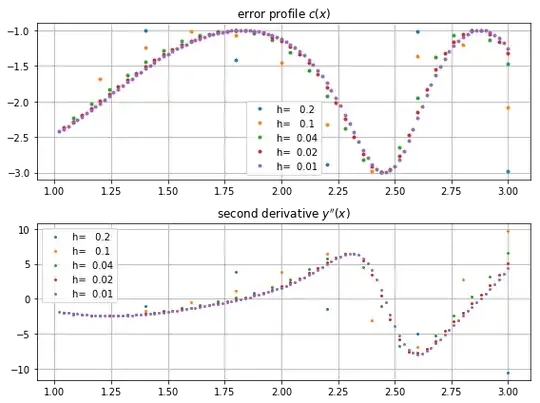
where $y_1=y_{2h}(x)$ are the values for $5$ steps with $2h=0.4$, $y_2=y_h(x)$ the corresponding values for a solution with $h=0.2$ and $c(x)=(y_{2h}(x)-y_h(x))/h$ is the estimate for the leading coefficient in $$y_h(x)=y_{\rm exact}(x)+c(x)h+O(h^2).$$ So with $|c(x)|\le 3$ one would need $h=10^{-3}/3$ for the goal of the task.

The theoretical bound will lead to a radically smaller bound for $h$.

(after the discussion in comments below the question)

The value you get from the cited formula is correct, I got the same value for my last remark above. Note that the theoretical bound is in all steps of its derivation strictly pessimistic to apply to all possible situations. In practice the contributions are not always maximum and some local errors may have opposite sign and thus partially cancel out.

With some care one can show that $|y′′(x)|≤12$, but that improves the bound only by a factor of about $3$. At all points $f(x,y)\in[1,3]$, so for any solution $x-1\le y(x)-y_0\le 3(x-1)$, next $y''(x)=Df(x,y)=f_x+f_yf=-\cos(xy)(y+xf(x,y))$, so on this wedge you get $Df\in [-1,1]\cdot([-0.5,5.5]+[1,2]\cdot[1,3])\subset[-11.5,11.5]$.

My answer contains an a-posteriory estimate of the error behavior, essentially extrapolated from 2 points, but still surprisingly accurate. Plotting the estimates for a range of step sizes shows how stable this estimate is and how it evolves with $x$. As one can see, there is no visible exponential growth in this span of the solution.

enter image description here

Lutz Lehmann
  • 131,652