8

How to represent the calculation in this image mathematically?

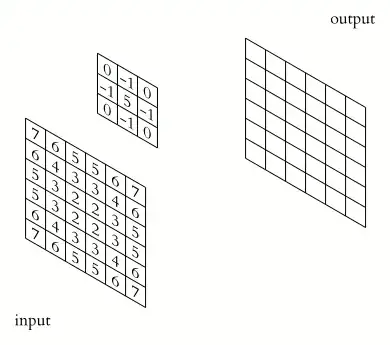
enter image description here

For example: With the discrete convolution and Fourier Transform.

It tries to do a calculation on the original image (image $A$/input) and save the result of the calculation in image $B$/output. It tries to multiply the pixel you are dealing with, with $5$ and it tries to multiply one pixel at the left, one pixel at the right, one pixel above of it and one pixel under it with $-1$ and adds the value of all the $5$ pixels you just multiplied together. After that, it will save the value of the new pixel in picture $B$. This happens to every single pixel in the image. Since there are no surrounding pixel on the corners, it simply takes them from somewhere else.

Which makes more sense?






Solution A:

$c(i,j) = \displaystyle\sum_{k_1 \in \Bbb N} \displaystyle\sum_{k_2 \in \Bbb N} a(k_1, k_2) b(i - k_1, j - k_2)$ where $a$ and $b$ are your matrices.

Supposing $a$ is your picture, by setting $b(0,0)=5$, $b(±1,0)=−1$, $b(0,±1)=−1$ and $b=0$ elsewhere.







Solution B:

$$ (f \ast g)(x,y) = \sum_{i=-\infty}^\infty \sum_{j=-\infty}^\infty f(i,j) g(x-i,y-j). $$ $f$ is the filter, $g$ is the image, and $f \ast g$ is the filtered image. We have $f(0,0) = 5$, $f(-1,0) = f(1,0) = f(0,-1) = f(0,1) = -1$, and $f(i,j) = 0$ otherwise.




Note to answerer: Please try not to overcomplicate your answer...

simonet
  • 467
user1095332
  • 321
  • nice animation interesting.+1 – dato datuashvili Apr 07 '13 at 09:11
  • i think it is called Walsh-Hadamard Transform,is not it? – dato datuashvili Apr 07 '13 at 09:12
  • http://en.wikipedia.org/wiki/Kernel_(image_processing) – dato datuashvili Apr 07 '13 at 09:16
  • @dato That doesn't explain how te represent it with a discrete convolution? – user1095332 Apr 07 '13 at 09:17
  • @user1095332 Aren't you answering your own question? The way to represent this process is through a discrete convolution. One function $f : \Bbb N^2 \rightarrow \Bbb R$ represents the image and another $g : \Bbb N^2 \rightarrow \Bbb R$ represents the convolution operator which is defined on a small support $[-1, 1] \times [-1, 1]$. See http://mrl.nyu.edu/~dzorin/intro-graphics/handouts/filtering/node7.html for explicit formula. – muzzlator Apr 07 '13 at 10:06
  • @muzzlator The problem I have is A. How to represent the matrix correctly, when using the Two-dimensional discrete convolution formula... You have to break it up in 2 onedimensional arrays (one for the y-direction and one for the x-direction)... How to break it up? and B. How to represent the multiplication and adding the value together. This is a 2D convolution. You only multiply by 5 once and not twice. You have to multiply a surrounding pixel with -1 and add that to the pixel you multipled with 5. How do you represent that with the formula? – user1095332 Apr 07 '13 at 10:20
  • @muzzlator How to multiply one pixel by 5 and multiply 4 pixels with -1 and add those together? – user1095332 Apr 07 '13 at 10:37
  • 2
    That website I linked to shows a mathematical description of the formula. You don't need to break it up into a series of two one dimensional convolutions. $$c(i,j) = \displaystyle\sum_{k_1 \in \Bbb N} \displaystyle\sum_{k_2 \in \Bbb N} a(k_1, k_2) b(i - k_1, j - k_2)$$ where $a$ and $b$ are your matrices. Supposing $a$ is your picture, by setting $b(0,0) = 5, b(\pm 1, 0) = -1$ and $b(0, \pm 1) = -1$ and $b = 0$ elsewhere, you will get the desired effect. – muzzlator Apr 07 '13 at 10:39
  • @muzzlator b is the kernel and a is the original image? When you say b(0,0)=5, it looks like you are trying to set the pixel value output for 0 on the x-axes and 0 on the y-axes to 5. This is really confusing, because this is true when you say $f(x)=x^2+5$. $f(0)=5$. And what do k1 and k2 stand for? – user1095332 Apr 07 '13 at 11:19
  • When he says $b(0,0)=5$ he is considering a $3\times 3$ matrix $b$ (your kernel) indexed by two integers in ${-1,0,1}$, so that $b(0,0)=b_{0,0}$ is the central element. In the formula $a$ is the input matrix, $b$ is the kernel, and $c$ is the output matrix. The integers $k_1,k_2$ are just indexes; you should actually let them take values which make sense for finite dimensional matrices (or let be $0$ the "out of bounds" entries of $a$ and $b$), though. – A.P. Apr 07 '13 at 11:36
  • Actually, that's what you were asking for: a formula to represent the values of the output pixel with coordinates $(x,y)$ given the values of an input and a kernel matrices. If this is not what you were looking for could you state your question differently, please? – A.P. Apr 07 '13 at 11:44
  • @A.P. When you pass -1,0 to function b. Does -1 replace i and does 0 replace j? – user1095332 Apr 07 '13 at 12:40
  • Yes. Note that, although you can see $b(i,j)$ as a function, it could be easier to think of it as the entry of matrix $b$ at row $i$ and column $j$. – A.P. Apr 07 '13 at 12:43
  • @A.P. So, does that mean that the i and j in c(i,j) are not equal to the i and j in b(i,j)? – user1095332 Apr 07 '13 at 12:53
  • let us continue this discussion in chat – A.P. Apr 07 '13 at 13:35
  • @muzzlator Wouldn't it make more sense to make k1 and k2 an element of Z? And take the sum from minus infinity to plus infinity? Make a the filter and b the picture? And take a(0,0)=5, a(±1,0)=−1 and a(0,±1)=−1 and a=0 elsewhere? – user1095332 Apr 07 '13 at 16:20
  • @user1095332 Sorry yes, I meant $\Bbb Z$, nicely spotted – muzzlator Apr 08 '13 at 00:32

1 Answers1

3

Let $A$ be an $m\times n$ matrix representing the input image, and $K$ be an $s\times t$ matrix representing the kernel, with $s$ and $t$ odd (since we need it to have a central entry). We will index $A$ with $$(i,j)\in \{1,\dotsc,m\}\times\{1,\dotsc,n\}$$ and we will index $K$ with $$(h,k)\in\left\{-\sigma, \dotsc, \sigma\right\}\times\left\{-\tau, \dotsc,\tau\right\}$$ where $\sigma=\left\lfloor \frac{s}{2}\right\rfloor$, $\tau=\left\lfloor \frac{t}{2}\right\rfloor$, and with $\lfloor \cdot \rfloor$ we mean the floor function. We do this so that the central entry of $K$ will have index $(h,k)=(0,0)$.

To take care of the edge entries we add two rows and two columns to $A$ by repeating the first and last row and column. That is, we define the extra entries $$ \begin{align} A(0,0)&:=A(1,1) & A(0,j)&:=A(1,j) & A(0,n+1)&:=A(1,n)\\ A(i,0)&:=A(i,1) & & & A(i,n+1)&:=A(i,n) \\ A(m+1,0)&:=A(m+1,1) & A(m+1,j)&:=A(m,j) & A(m+1,n+1)&:=A(m,n) \end{align} $$ This corresponds to the "extension" edge handling method. You can easily change those extra rows and columns to adapt to other methods.

Then for any fixed $(i,j)\in\{1,\dotsc,m\}\times\{1,\dotsc,n\}$ the entry $(i,j)$ of $K*A$ will be $$ (K*A)(i,j) = \sum_{h=-\sigma}^{\sigma}\sum_{k=-\tau}^{\tau} K(h,k)\;A(i+h,j+k) $$

A.P.
  • 9,906