10

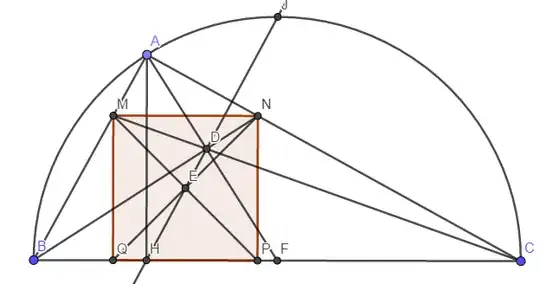
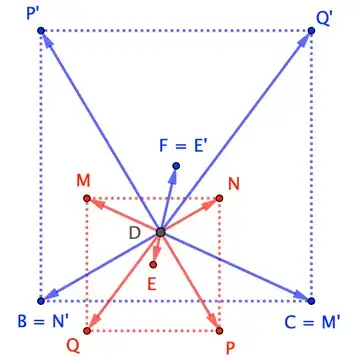
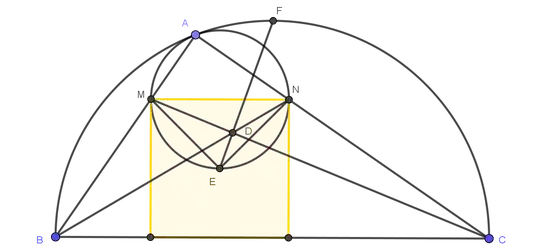
Let A be a point on a fixed semicircle with diameter BC. MNPQ is a square such that $M \in AB, N \in AC, P \in BC, Q \in BC$. Let D be the intersection of BN and CM and E be the center of the square. Prove that as A varies, DE always passes through a fixed point.

o

The fixed point is the midpoint of the semicircle. Any suggestion ?

Edit : I have proved that AE is the angle bisector of angle BAC and AD passes through the midpoint of BC.

I think that DE also passes through the feet of the altitude to BC. May be harmonic bundle is useful. (D,H,E,J) = -1 ? enter image description here

nonuser
  • 91,557
Kiên Phùng Hữu
  • 139
  • Welcome to Math.SE! The community here prefers/expects questions to include something of what the asker knows about the problem. (What have you tried? Where did you get stuck? etc) This information helps answerers tailor their responses to best serve you, without wasting time (theirs or yours) explaining things you already know or talking over your head. (It also helps convince people that you aren't simply trying to get them to do your homework for you.) Since comments are easily overlooked, edit your question to add your thoughts. – Blue Dec 22 '19 at 03:37
  • Thank you. Sorry, but I'm not quite good at geometry, so I want to learn more from you guys. – Kiên Phùng Hữu Dec 22 '19 at 03:55
  • 2
    Your update is very good. It's helpful to know, for instance, that you're aware of things like harmonic bundles. That said, I believe this problem has a simpler solution: Show that $D$ is the center of a dilation that takes $M$ to $C$ and $N$ to $B$. Consider the effects that dilation has on other points. – Blue Dec 22 '19 at 03:59
  • 1
    +1 for being one of the few who when told they need to add details about their own attempts, respond by adding those details. And doing a great job at it. – Paul Sinclair Dec 22 '19 at 17:12

4 Answers4

5

Expanding upon my comment ...

In fact, the semicircle and even half the elements of $\triangle ABC$ are irrelevant to the result. All that really matters is that $\square MNPQ$ is a square ---any square (barring degeneracies)--- such that $\overline{MN}\parallel\overline{BC}$. The construction's fixed point, which you have keenly observed is the midpoint of the semicircle, is, more simply, the center of a square erected upon $\overline{BC}$. (Below, we resolve the ambiguity of which of two candidate squares is meant.)

enter image description here

The parallelism condition guarantees $\triangle DBC\sim\triangle DNM$, so that $|DB|/|DN|=|DC|/|DM|$, making $D$ the center of a dilation/homothety that carries $N$ to $B$ (which my figure also denotes $N'$) and carries $M$ to $C=M'$. Necessarily, the dilated images $P'$ and $Q'$ of $P$ and $Q$ complete square $\square M'N'P'Q'$ as the dilated image of $\square MNPQ$. (Note: The fact that the squares have opposite orientations resolves the ambiguity mentioned above.) Thus also, the dilation carries center $E$ of one square to center $F=E'$ of the other; since a point and its dilated image are collinear with the center of dilation, we are done. $\square$

Blue
  • 83,939
1

Here is an easy coordinate geometric proof:

Let the radius of semicircle be $1$ and centre be $(0,0)$ without loss of generality, and the side length of the square be $a$. Then coordinates of $B$ are $(-1,0)$, coordinates of $C$ are $(1,0)$ and that of $M$ are $(b,a)$ for some $b$. Coordinates of $N$ are $(b+a,a)$ and coordinates of $E$ are $\left(b+\frac{a}{2},\frac{a}{2}\right)$. Equation of $BN$ is $$\frac{y}{x+1}=\frac{a}{a+b+1}$$ and equation of $CM$ is $$\frac{y}{x-1}=\frac{a}{b-1}$$ Solving these to find the coordinates of $D$, we get that the coordinates of $D$ are $\left(\frac{a+2b}{a+2},\frac{2a}{a+2}\right)$.

Now, we wish to show that $F(0,1),D$ and $E$ are collinear, so what we wish is as follows: $$\text{Slope of EF = Slope of ED}$$ $$\iff \frac{\frac{a}{2}-1}{\frac{a+2b}{2}}=\frac{\frac{a}{2}-\frac{2a}{a+2}}{\frac{a+2b}{2}-\frac{a+2b}{a+2}}$$ $$\iff a-2 = \frac{a^2+2a-4a}{a+2-2}$$ which is indeed true.

Martund
  • 14,826
  • 2
  • 14
  • 33
0

You have two diagrams that conflict on a few points so I'll just use the labeling in the second diagram.

You've already done some excellent work here. The key here is drawing the antipode of J. Let's call it X. Since you've proved that AE bisects A, it follows that AE passes through X. Furthermore, we can show that $\frac{AE}{EX}=\frac{AH}{XJ}$, which shows that E lies on $HJ$ (length chase with the homothety).

Now, we just need to show that $D$ also lies on this line. We can once again use ratios. You've already shown that $AD$ passes through the midpoint of $XJ$, $F$, which means we just need to prove $2\frac{AE}{EX}=\frac{AD}{DF}$ in order to show $D$ lies on $HEJ$. But from Menelaus' Theorem we have $\frac{AM}{MB}\frac{BC}{CF}\frac{FD}{DA}=1\implies \frac{AD}{DF}=2\frac{AM}{MB}$.

Thus, the condition simplifies into proving $\frac{AE}{EX}=\frac{AM}{MB}$, which is a direct result of the homothety we proved above, so we're done!

Alvin Chen
  • 571
0

Let $F$ halves arc $BC$. Let us prove $F$ is on $DE$.

Notice that $\angle MEN = 90^{\circ} = \angle MAN$ thus $AMEN$ is cyclic with diameter $MN$.

Since $ME = EN$ we see that $E$ halves arc $MN$ which does not contain $A$. enter image description here

Now observe a homothety at $D$ which takes $M\mapsto C$ and $N\mapsto B$.

So it take small circle to big. Now let it take $E$ to $E'$ (so $E,D,E'$ are colinear). Where is $E'$?

Since $E$ is on small circle $E'$ must be on big circle and thus halves arc $BC$ which contains $A$ so $E' = F$.

nonuser
  • 91,557