Prove that distance between orthocenter and incenter is $\sqrt{2r^2-4R^2\cos A\ cos B\cos C}$
My attempt is as follows:-
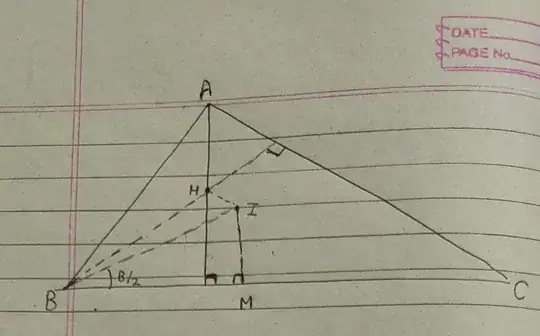
In the figure H denotes the orthocenter and I denotes incenter.
$IM=r$, $BH=2R\cos B$
In $\triangle IBM$
$$\dfrac{IB}{IM}=\mathrm{cosec} \frac{B}{2}$$ $$IB=r\mathrm{cosec} \frac{B}{2}$$ $$IB=4R\sin \frac{A}{2}\sin \frac{C}{2}$$
$\angle HBI=90-C-\dfrac{B}{2}$
Applying cosine rule in $\triangle IBH$
$$\cos \left(90-C-\dfrac{B}{2}\right)=\dfrac{BH^2+BI^2-HI^2}{2BH\cdot BI}$$
$$2\sin\left(C+\dfrac{B}{2}\right)\cdot2R\cos B\cdot4R\sin\frac{A}{2}\sin\frac{C}{2}=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-HI^2$$
$$HI^2=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\sin\left(C+\dfrac{B}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}$$
$$HI^2=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\sin\left(\dfrac{2C+B}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}$$
$$HI^2=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\sin\left(\dfrac{2C+\pi-A-C}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}$$
$$HI^2=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\sin\left(\dfrac{\pi}{2}-\dfrac{A}{2}+\dfrac{C}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}$$
$$HI^2=4R^2\cos^2B+16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-16R^2\cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)\cdot\cos B\cdot\sin\frac{A}{2}\sin\frac{C}{2}+4R^2\cos^2B$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(4\cos\left(\dfrac{A}{2}-\dfrac{C}{2}\right)\cdot\sin\frac{A}{2}\sin\frac{C}{2}-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(4\sin\frac{A}{2}\sin\frac{C}{2}\left(\cos\frac{A}{2}\cos\frac{C}{2}+\sin\frac{A}{2}\sin\frac{C}{2}\right)-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(4\sin\frac{A}{2}\sin\frac{C}{2}\cos\frac{A}{2}\cos\frac{C}{2}+4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(\sin A\sin C+4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(\sin A\sin C+(1-\cos A)(1-\cos C)-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(\sin A\sin C+1-\cos C-\cos A+\cos A\cos C-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(1-\cos C-\cos A+\cos A\cos C+\sin A\sin C-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\left(1-\cos C-\cos A+\cos A\cos C+\sin A\sin C-\cos B\right)$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4R^2\cos B\cos A\cos C-4R^2\cos B\left(1-\cos C-\cos A+\sin A\sin C-\cos B\right)$$
$$HI^2=4R^2\left(4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\left(1-\cos C-\cos A+\sin A\sin C-\cos B\right)\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=4R^2\left(4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\left(1-\cos C-\cos A+\sin A\sin C-\cos (\pi-A-C)\right)\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=4R^2\left(4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\left(1-\cos C-\cos A+\sin A\sin C+\cos A\cos C-\sin A\sin C\right)\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=4R^2\left(4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-\cos B\left(1-\cos C-\cos A+\cos A\cos C\right)\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=4R^2\left(4\sin^2\frac{A}{2}\sin^2\frac{C}{2}-4\cos B\sin^2 \frac{A}{2}\sin^2\frac{C}{2}\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=16R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}\left(1-\cos B\right)-4R^2\cos B\cos A\cos C$$
$$HI^2=32R^2\sin^2\frac{A}{2}\sin^2\frac{C}{2}\sin^2\frac{B}{2}-4R^2\cos B\cos A\cos C$$
$$HI^2=2r^2-4R^2\cos B\cos A\cos C$$ $$HI=\sqrt{2r^2-4R^2\cos B\cos A\cos C}$$
This proof got very long, any simple way to prove this?