General solutions of $x+y+z=x^2+y^2+z^2=x^3+y^3+z^3$

Question

Note: this actually has nothing to do with probability theory. Fell free to skip ahead and solve the equations below.

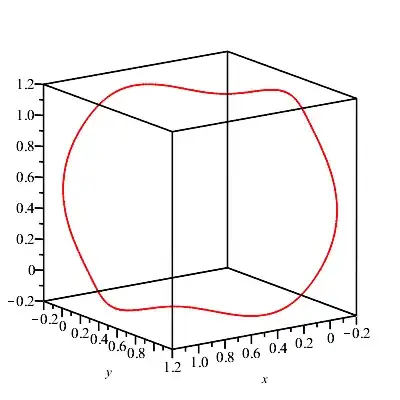
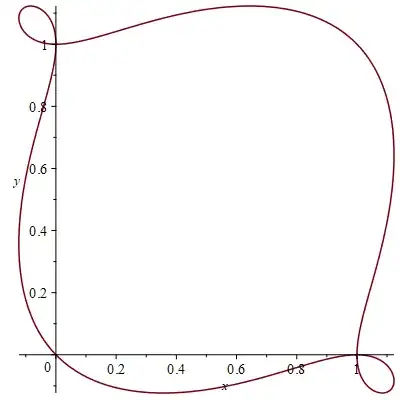
Since I am unable to solve this continuous version of a problem about moments, I am now trying to do something simple but related. Let's say $X$ is a random variable which can take three values $x,y,z$ with probability $1/3$ each. For what values of $x,y,z$ does $X$ have its first, second and third central moments equal?

That is, how to solve the system of equations $$ x+y+z=x^2+y^2+z^2=x^3+y^3+z^3? $$ The first two equations give a sphere which just covers the unit cube $0<|x|,|y|,|z|<1$. But the second equation is harder to tackle. I guess that we can only have trivial solutions at $x,y,z=0,1$, but I am not sure. Writing $p=x+y+z$, we get a cubic with solution $x,y,z$: $$ u^3-pu^2+\frac12 p(p-1)u-\frac{1}{12}p(p-1)(p-2) =0, $$ but that doesn't seem to help.

You could apply newton identities to set up the cubic and have solutions as the roots. — Calvin Lin, Dec 05 '19 at 03:30
One solution is $x=\frac12=0.5, y=\frac12 +\sqrt{\frac38}\approx 1.11237243569579, z= \frac12 -\sqrt{\frac38}\approx -0.11237243569579$ — Henry, Dec 05 '19 at 04:36

score 2 · Answer 1 · answered Dec 05 '19 at 03:11

2

You have two equations in three variables, so this should describe a curve in space.

It looks like this, according to Maple:

The resultant of $x+y+z-(x^2+y^2+z^2)$ and $x+y+z-(x^3+y^3+z^3)$ with respect to $z$ is the rather fearsome $$ -2\,{x}^{6}-3\,{x}^{4}{y}^{2}-2\,{x}^{3}{y}^{3}-3\,{x}^{2}{y}^{4}-2\,{ y}^{6}+6\,{x}^{5}+3\,{x}^{4}y+9\,{x}^{3}{y}^{2}+9\,{x}^{2}{y}^{3}+3\,x {y}^{4}+6\,{y}^{5}-6\,{x}^{4}-7\,{x}^{3}y-10\,{x}^{2}{y}^{2}-7\,x{y}^{ 3}-6\,{y}^{4}+2\,{x}^{3}+4\,{x}^{2}y+4\,x{y}^{2}+2\,{y}^{3} $$ That $=0$ describes the projection of this curve on the $xy$ plane. It looks like this:

answered Dec 05 '19 at 03:11

Robert Israel

470,583

So...there is no simple way to describe the solution curve? – Ma Joad Dec 05 '19 at 03:12
Your curve seems to miss $(0,0,0)$ and $(1,1,1)$ – Henry Dec 05 '19 at 04:43
@Henry Indeed, it seems those are isolated points where the surfaces $x+y+z - (x^2 + y^2 + z^2)$ and $x+y+z-(x^3 + y^3 + z^3)$ are tangent to each other. – Robert Israel Dec 05 '19 at 14:11

score 2 · Answer 2 · answered Dec 05 '19 at 04:45

2

Let the values be equal to $t$.

Then $xy+yz+zx = \frac{ (x+y+z)^2 - (x^2+y^2+z^2) }{2} = \frac{t^2-t}{2}$
and $xyz = \frac{ (x+y+z)^3 - (x^3+y^3+z^3) - 3(xy+yz+zx)(x+y+z)}{-3} = \frac{t^3-t - 3(t^2-t)/2 \times t}{-3} = \frac{-t^3+3t^2 - 2t } { 6}$.

So, these are roots to the cubic

$$X^3 - 6tX^2 + 3(t^2-t)X+(t^3-3t^2+2t) = 0.$$

We could then obtain the solutions via the cubic formula:

answered Dec 05 '19 at 04:45

Calvin Lin

77,541

Interesting that $xy+yz+zx = \frac{ (x+y+z)^2 - (x^2+y^2+z^2) }{2} = \frac{t^2-t}{2}=t(t-1)/2$ and $xyz = \frac{ (x+y+z)^3 - (x^3+y^3+z^3) - 3(xy+yz+zx)(x+y+z)}{-3} = \frac{t^3-t - 3(t^2-t)/2 \times t}{-3} = \frac{-t^3+3t^2 - 2t } { 6}=-t(t-1)(t-2)/6$. – marty cohen Dec 05 '19 at 05:12

General solutions of $x+y+z=x^2+y^2+z^2=x^3+y^3+z^3$

2 Answers2