We give a detailed example solution for the smaller 2x2x2-cube. From this you can easily deduce the procedure for larger nxnxn-cubes.
It might be useful to turn the algorithm presented here into a computer program, but this is not part of this solution.
Here we go:
First you need to decide how you designate a state of the cube. You could use David Singmaster's twisted cycles but it is conceptually simpler (we don't need to speak about orientations of corners and edges) to consider the 2x2x2 cube as a collection of $6$ faces times $4$ stickers $= 24$ stickers in total.
Let us adopt the following numbering system for the stickers of the faces
$f=\left(
\begin{array}{cc}
1 & 2 \\
3 & 4 \\
\end{array}
\right)\;
r=\left(
\begin{array}{cc}
5 & 6 \\
7 & 8 \\
\end{array}
\right)
b=\left(
\begin{array}{cc}
9 & 10 \\
11 & 12 \\
\end{array}
\right)\;\\
l=\left(
\begin{array}{cc}
13 & 14 \\
15 & 16 \\
\end{array}
\right)\;
u=\left(
\begin{array}{cc}
17 & 18 \\
19 & 20 \\
\end{array}
\right)\;
d=\left(
\begin{array}{cc}
21 & 22 \\
23 & 24 \\
\end{array}
\right)$
Now we notice that every state of the cube is a permutation of these 24 stickers.
In the beginning you have the state where each sticker is in its position. We denote that in cycle notation as (k), as a collection of cycles of the stickers onto itself, viz.
$e = (1)(2)(3)...(24)$
As an example of non trivial permutations let us consider the permutations caused by two moves $R$ and $U$.
Carefully watching the replacements of the stickers we find that the move $R$ takes $2\to 18\to 11 \to 22$ and back to $2$, $4\to 20\to 9 \to 24$ and back to $4$, and $7\to5\to6\to8$ and back to $7$.
Hence
$R = (2, 18, 11, 22)(4,20,9,24)(7,5,6,8)$
and the move $U$ is
$U = (1, 13, 9, 5)(2,14,10,6)(20,19,17,18)$
and similarly for the remaining 4 moves.
Now consider the process (combination of moves) $RU$ which understood here as carrying out first $R$, and then $U$.
We don't need to look to the cube anymore but just at the cycles of the two moves.
Let us look where sticker $4$ moves with $RU$:
$R$ takes $4$ to $20$, then $U$ takes $20$ to $19$ and so on. We write this as
$(R: 4 \to 20$, $U: 20 \to 19$, $R: 19 \to 19$, $U: 19 \to 17$, $R: 17 \to 17$, $U: 17 \to 18$, $R: 18 \to 11$, $U: 11 \to 11$, $R: 11 \to 22$ and so on
Finally the cycle including $4$ is
$(13, 9, 24, 4, 19, 17, 18, 11, 22, 14, 10, 6, 8, 7, 1)$
it has length 15.
Now we look for remaining numbers. We find 2, trace it similarly and get the cycle
$(20, 5, 2)$
It has length 3, and can be identified as the $\frac{1}{3}$ rotation of the corner (fur).
The remaining 6 numbers lead to cycles of length 1.
Now we are finished and have obtained the cyle representation
$P_1 = RU = (13, 9, 24, 4, 19, 17, 18, 11, 22, 14, 10, 6, 8, 7, 1)(20, 5, 2)$
Here we have dropped the trivial cylcles of length 1
The order is equal to the LCM of the lengths of the cyles, which here is LCM(15,3) = 15.
Doing a similar analysis with the move $R^2 U$ ee get
$P_2 = R^2 U = (13, 9, 4, 5, 8, 1)(11, 14, 10, 6, 7, 2){18, 22, 20, 24, 19, 17)$
Each of the tree cycles have length 6, hence the order is 6.
If you do the same for the 3^3 cube you will find that the process of J. B. Butler
$P_{501} = RU^2D^{-1}BD^{-1}$
has order $1260 = 2^2\cdot 3^2 \cdot5 \cdot7$. This turns out to be the maximum order for the 3^3 cube.
Remark: the numbering of this process was adopted in my book "Der ungarische Zauberwürfel" published in 1982.
Exercise
You might wish to calculate the orders of all 9 processes of the type $R^a\cdot U^b$ with $a, b=1,2,3$ by calculating their cycle representations.
Answer: the list of orders is $(15, 6, 9, 6, 3, 6, 9, 6, 15)$.
Specific results
I have written a simple Mathematica code to treat the permutations in the 48 dimensional framework.
Task 1:
Find as many possible orders with the most simple ingredients. To this end we calculate the orders of all processes which can be constructed from $n$ factors $U$ and $n$ factors $R$ in all possible orders, with $1\le n \le 8$. Here's the list of all orders that appear
$\{1,2,3,(4,)5,6,9,10,12,15,18,20,21,30,35,36,42,45,60,63,105\}$
Notice that the order $4$ appears only for $R$ and $U$ itself.
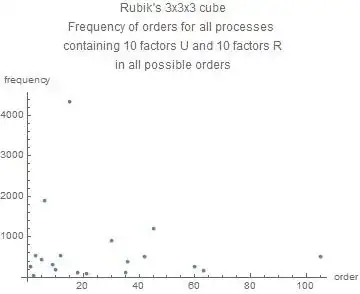
The frequency of orders for $:U^{10} R^{10}:$ is shown in the follwing picture