Summary
Is it possible to beat an "Impossible" Ultimate tic-tac-toe in less than $18$ moves?
The "Impossible" references playing against an AI that uses a depth $d=8$ min-max search with a "potential 3-in-a-row" evaluation function (see more details below.)
You can play against it here, against difficulties ranging from $d=1$ to $d=8$.
I managed to beat it in $18$ moves with both $X$ and $O$ (see more details below).
I'm curious if it is possible to beat it in $17$ or less moves, with either $X$ or $O$?
Game rules and notation
Ultimate tic-tac-toe ($\text{UT3}$) is a game composed of nine regular tic-tac-toe boards.
Nine regular tic-tac-toe boards are set up to represent one "ultimate tic-tac-toe board".
Each regular board has nine tiles into which players 1., 2. can play into (X, O pieces). Each move is played into one of the nine "boards", into one of the nine "tiles". Hence, we introduce the notation for a move as $(n,m)$ for (board, tile) where: $$n,m\in\{\text{N},\text{NE},\text{E},\text{SE},\text{S},\text{SW},\text{W},\text{NW},\text{C}\}$$ Stand for eight compass directions ("north", "northeast", ...) and C as "center". When a player plays into $(n_0, m_0)$, his opponent now must play into $(m_0, m_1)$ where $m_1$ is any empty tile inside $m_0$ board. That is, the previous tile played determines the next board into which we must play. Unless, board $m_0$ is full, then, player can choose any other board.
Additionally, you can't play into captured boards. If you need to play into a board that you can't play in (it is full or captured), then you are allowed to play in any other board, regardless of what the last tile move was.
Capturing a board simply means to make 3-in-a-row tiles inside it (regular tic-tac-toe). The goal is to capture 3-in-a-row boards, to win the global (ultimate) tic-tac-toe game.
This game was discussed on MSE some years ago.
The optimal strategy for Ultimate tic-tac-toe is not known. (Optimal strategy is known under the "simpler" variation where players are still forced to play into the "captured" boards, instead of letting them choose another board.)
As of this moment, I'm not aware of any references or works that try to find strategies for this game. The only things I've seen are AI implementations ranging from min-max algorithms and monte carlo simulations to simple neural networks.
There is one implementation of such computational strategy I found to be fun.
Min-max AI that counts potential 3-in-a-row's
Say your opponent is a min-max algorithm with depth $d$ (goes $d$ moves into the game tree).
Min-max algorithm uses a value (evaluation) function $f$ that takes in the game state and returns the evaluated score of the game position. One such function we are interested in, is:
$$ f(G)=\sum_{L\in G} v(L) $$
Where $G$ is the game state, and the RHS sum goes over all "lines" $L$ (columns, diagonals, rows). The $v(L)$ gives score $0$ if the line $L$ contains both X's and O's. Otherwise, it returns the number of X's (or O's) in that line. The $v$ can be taken to be positive when counting your pieces and negative when counting the opponent's pieces.
Such AI is completely deterministic and determined by the depth and game state. Hence, it will always respond the same to the same sequences of moves.
You can play against such AI online as either X or O, versus depths $d=1,2,\dots,8$ that determine the difficulty and are named "Piece of cake, Medium, ..., Impossible". This was made by bennett-zhang and is open source on github.
In other words, here is the bennett-zhang's comment on their implementation of such AI:
The program uses the minimax algorithm with alpha-beta pruning in order to create a search tree of possible moves, then evaluates the state of the game after each move and picks the move which scores the highest.
...
To evaluate the game state and determine how well each player is doing, the program looks at every possible "line", that is, row, column, or diagonal. If the line contains only X's or only O's, the line is assigned a score based on the number of X's or O's it contains. Otherwise, the line's score is set to zero. Every time a move is made inside of a cell, the lines containing that cell have their score updated.
The challenge (The question)
I was wondering if it is possible to find the minimal moves needed, to beat such AI?
That is, we are allowed to play as either X (first) or O (second). The number of moves (your own pieces) you played is being counted, and lets call it $N(d)$.
Trivially, $N(d)\ge 9$ since you need to capture at least three boards to win, and in each of those, place at least three pieces to make 3-in-a-row, which totals to $3\cdot3=9$.
I'm interested in $d=8$ (The "impossible" difficulty when playing the game) $(*)$.
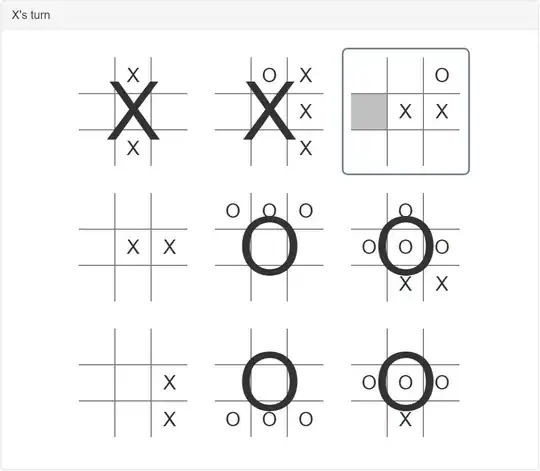
So far, I managed to find a wins in $18$ moves with both $X$ and $O$. The moves are:
X18: (NW/C), C*2, W, S*2, SE, S, (NW/E), SE, NE, SE, E*4, SE, (N, W).
O18: (C/C), NE, S*3, E, W*3, SE*3, SW, NW, NE, (NE, NW), (SW, SE), NE.
Where M*3 represents playing into tile M three times in a row. Some moves are given as just tiles M, instead of (board, tile)=(N, M) pairs, since the board is predetermined in those cases.
The following image gives the look of the board for corresponding $18$-move games:
Based on playing the game on the provided link on difficulty "Impossible".