Alternative method:
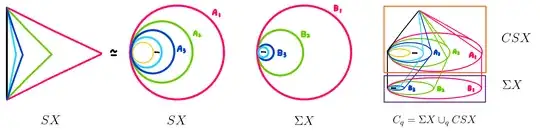
Let $U=C(SX)$, $V$ be mapping cylinder of $q$, $V=SX \times I \sqcup \Sigma X /\sim$, i.e. $(x,1)\sim q(x)$ for $x\in SX$.
Let $W$ to be space by gluing $U$ and $V$ along $SX$.
$V$ deformation retracts to $\Sigma X$, so $C_q=\Sigma X \cup_q C(SX) \simeq W$.
$\pi_1(U)=0$. Let $i_1: SX \hookrightarrow C(SX)=U$, $i_2: SX \hookrightarrow V$.
$i_{1*}=0$, $i_{2*}:\pi_1(SX)\to\pi_1(V)\cong\pi_1(\Sigma X)$.
From van Kampen's theorem, $\pi_1(W)\cong\pi_1(U)*\pi_1(V)/N$, $N$ is generated by $i_{1*}(w)i_{2*}(w^{-1})$ for all $w\in \pi_1(SX)$. $\pi_1(W)\cong \pi_1(\Sigma X)/\pi_1(SX)$.
Let $\rho$ be the surjective homomorphism $\pi_1(\Sigma X) \to \prod_\infty \mathbb Z$ given in page 49 of Hatcher.
$\color{red}{\text{$\rho$ maps $\pi_1(SX)$ to $\bigoplus_\infty \mathbb Z$} \ (*) }$ , so $\rho$ induces a surjective homomorphism
$\pi_1(\Sigma X)/\pi_1(SX) \to \prod_\infty \mathbb Z/\bigoplus_\infty \mathbb Z$. $\quad\Box$
Claim $(*)$ in red is remained to check.
I tried to give an explicit expression of $\rho$ to prove claim $(*)$ in the question, but I couldn't fully prove the well-defineness of the $\rho$ I constructed.
My former proof (wrong):
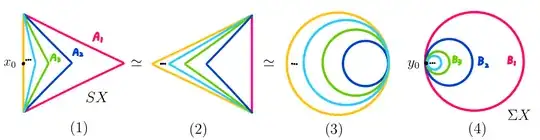
$1$. Yellow circle doesn't belong to $SX$. It means the lower bound of circles in $SX$.
Circles in $\Sigma X$ have no such lower bound. Region containing "$\cdots$" means there're countably many circles in it.
From outside to inside, circles in $SX$ and $\Sigma X$ are denoted by $A_n$ and $B_n$ with common point $x_0$ and $y_0$.
Quotient map is $q:SX \to \Sigma X$, mapping cone $C_q=\Sigma X \cup_q CSX$.
$2$. Choose basepoint of loops at $x_0\sim y_0$. $A_i\sim B_i$, so loop around $A_i$ can be considered as loop around $B_i$.
For $[f]\in \pi_1(C_q)$, if $f$ wraps $a_n$ times around circle $B_n$ clockwise, let $\tilde f: I \to SX$ wrap $a_n$ times around circle $A_n$ clockwise the same ways as $f$. Note that $q \circ\tilde f=f$.
Define $\varphi: \pi_1(C_q)\to \prod_\infty \mathbb Z/\bigoplus_\infty \mathbb Z,\ [f]\mapsto \overline{(a_n)_{n=1}^{\infty}}$.
$3$. If $(a_n)_{n=1}^{\infty} \in \bigoplus_\infty \mathbb Z$, then only finite $a_n$ is nonzero and $\tilde f$ is continuous on $I$, so $\tilde f$ is indeed a loop in $C_q$.
$[\tilde f]=[q\circ \tilde f]=[f]$. Note that $A_n\subset SX \subset CSX$ is contractible, so $[\tilde f]=0=[f]$, $f$ is nullhomotopic. $\pi_1([f])=\overline 0$.
This is consistent with $\overline{(a_n)_{n=1}^{\infty}}=\overline 0$ in $\prod_\infty \mathbb Z/\bigoplus_\infty \mathbb Z$.
If $(a_n)_{n=1}^{\infty} \in \prod_\infty \mathbb Z - \bigoplus_\infty \mathbb Z$, then $\tilde f$ is not continuous at $1$, so it's not a loop in $SX$ and $\color{red}{\text{ $f$ isn't nullhomotopic}}$.
$3$. $\varphi: \pi_1(C_q)\to \prod_\infty \mathbb Z/\bigoplus_\infty \mathbb Z$ is well-defined.
If $[f]=[g]$ in $\pi_1(C_q)$, $f, g$ wraps $a_n, b_n$ times around circle $B_n$ clockwise, then $f\circ g^{-1}$ wraps $a_n - b_n$ times around circle $B_n$ clockwise.
$f\circ g$ is nullhomotopic, so $(a_n-b_n)_{n=1}^\infty\in \bigoplus_\infty \mathbb Z$.
$\varphi([f])=\overline{(a_n)_{n=1}^{\infty}}=\overline{(a_n-b_n+b_n)_{n=1}^{\infty}}=\overline{(a_n-b_n)_{n=1}^{\infty}}+\overline{(b_n)_{n=1}^{\infty}}=\overline{(b_n)_{n=1}^{\infty}}=\varphi([g])$.
$\varphi$ is a well-defined surjective homomorphism. $\quad\Box$