Optimisation without calculus

Question

I am a tutor and a year 8 student of mine has been given a maths test question that I can not fathom how to solve and explain for the year level he is at. It asks about a piece of luggage that has the requirements of the 3 dimensions totalling no more than 270cm when added together. It then asks what is the maximum possible volume a suitcase could have without exceeding this requirement. Optimisation generally involves calculus which would be far beyond this grade. The teachers answer is Vmax length=width=depth which means 90x90x90=729,000cm^3 she offers no information though as to how these 3 numbers were selected to give the optimum volume. What am I missing?? Or am I overthinking it?

Answer 1

This is simply a basic application of the AM-GM inequality.

If we label our dimensions $w,l,h$, we seek to maximize $wlh$ under the condition that $w+l+h=270$. Note that by AM-GM$$\frac{w+l+h}3\geq\sqrt[3]{wlh}$$$$wlh\leq90^3$$

But this implies that $w,l,h=90$ maximizes $wlh$.

Answer 2

Even though the AM-GM inequality gives the shortest solution, it may be beneficial to try to develop some intuition for optimization as a preliminary step for calculus. For example, let $w+l+h$ be fixed, and assume that $h>0$ is also fixed for now. Let us change $w$ and $l$ a little bit from current values and see if we can get a larger volume, i.e. take $w+\epsilon$ and $l-\epsilon$ (as the sum should stay constant). Then we get the new volume to be $$ (w+\epsilon)(l-\epsilon)h=wlh+\epsilon(l-w)h-\epsilon^2h=wlh+\epsilon(l-w-\epsilon)h. $$ The next step is crucial: let the kid figure out that if $l\ne w$ then the volume can be increased for all small choices of $\epsilon$. For example, if $l-w>0$ then $l-w-\epsilon>0$ for all $0<\epsilon<l-w$ and, hence, the term $\epsilon(l-w-\epsilon)h$ is strictly positive, implying the increase of the volume. Similarly for $l-w<0$. Therefore, for the optimal choice it must be $w=l$. Repeating the argument for other pair of variables leads to all three must be equal.

Basically, the problem boils down to maximizing the expression $$ (w+\epsilon)(l-\epsilon)=wl+\epsilon(l-w)-\epsilon^2 $$ which can be done by completing the square in $\epsilon$ $$ wl+\epsilon(l-w)-\epsilon^2=\left(\frac{l+w}{2}\right)^2-\left(\frac{l-w}{2}-\epsilon\right)^2 $$ where the largest value is obviously when the last square is zero. Treating a general second order polynomial $ax^2+bx+c$, parabolas and its vertices, by completing the square is certainly a part of 8th grade curriculum.

Answer 3

Take any box with none of the sides equal, $x+y+z=270$ and volume $V_1$. Observe now $$V_1=xyz=\underbrace{(xy)}_{\text{face area}}\cdot z$$ Since $z$ is fixed, so is $x+y$. Your students can prove, that we can now construct another box, with a greater volume $V_2$, if we let $x=y$. This follows from the simple fact that, given a perimeter, the square englobes the biggest area among all rectangles.

Thus, among all rectangular solids with $x+y+z=270$ and a fixed $z$, the one with $x=y$ has the greatest volume. By a similar argument, if $x$ is fixed, we achieve the greatest volume for $z=y$. Therefore, the greatest volume is reached if $x=y=z=90$.

Please note that this "proof" is far from rigorous, whereas understandable enough for your students...

Answer 4

In Elements, VI, 27 Euclid maximizes a certain parallelogram, as a preliminary to the two very important theorems which follow--the geometric solution of quadratic equations in VI 28 & 29.

VI, 27: "Of all the parallelograms applied to the same straight line and deficient by parallelogrammic figures similar and similarly situated to that described on the half of the straight line, that parallelogram is greatest which is applied to the half of the straight line and is similar to the defect."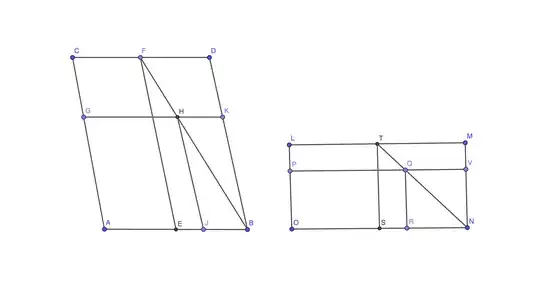

In the figure on the left, then, where $E$ bisects $AB$, Euclid proves that $AF$, "deficient" by $ED$, is greatest in area. He shows that any other parallelogram, such as $AH$, deficient by $JK$ similar to $ED$, is less than $AF$.

This may seem inapplicable to our problem since generally $AF$ and $AH$ are unequal not only in area but in perimeter. But in the figure on the right, where $OT$ is a square, the conditions of the problem are met: since $LP=RS$, then $LO+OS$ in the square equals $PO+OR$ in the rectangle.

Thus of all rectangles having the same perimeter, a square has the greatest area. Euclid does not generalize this to three dimensions in the solid books of Elements, but it seems clear that what holds for parallelograms in plane geometry will hold analogously for parallelepipeds in solid geometry, so that the cube will be the greatest in volume of all rectangular solids whose three dimensions sum to the same given amount.

I don't suppose eighth-graders study Euclid now, but they could do so of course, without calculus.