Can anyone advise me on how to derive a conformal map for this mapping? I am familiar with how to apply Schwarz-Christoffel from the upper half plane to the quadrilateral, but how do I then map from the quadrilateral to the sector?
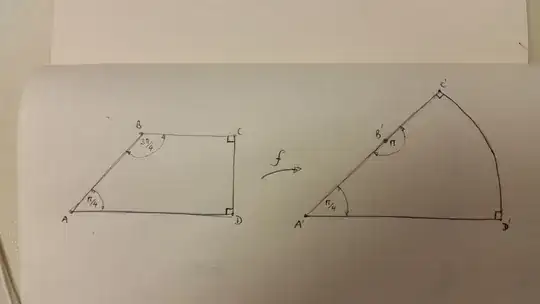
Can anyone advise me on how to derive a conformal map for this mapping? I am familiar with how to apply Schwarz-Christoffel from the upper half plane to the quadrilateral, but how do I then map from the quadrilateral to the sector?

If we start with the sector with the angle $\pi/4$, then $z^8$ maps it to $\mathbb D \setminus [0, 1)$. The Joukowsky transform maps $\mathbb D \setminus [0, 1)$ to $\mathbb C \setminus [-1, \infty)$. A branch of $\sqrt {z + 1}$ maps $\mathbb C \setminus [-1, \infty)$ to the upper half-plane. By the Schwarz-Christoffel formula, a branch of $z^{1/4} \hspace {1.5px} {_2 F_1}(1/8, 1/2; 9/8; z^2)$ maps the upper half-plane to a quadrilateral with the given angles. Then we have to take the inverse of the resulting composition of mappings.
If we want to get a quadrilateral similar to the given one, the problem is more difficult, because only three of four points on the real axis can be chosen arbitrarily.
How would I go about deriving a 'continuous' (but not necessarily conformal) mapping for the above? Would that be a lot simpler? The map should not significantly distort/stretch shapes (so the ideal case would be conformality, but this is not necessary).
– niran90 Dec 03 '19 at 07:36