0

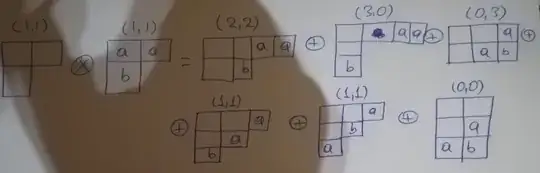
We can represent a tensor with $(n, m)$ where $n$ are the upper indices and $m$ the lower ones. If I get the direct product of $(n,m)\otimes (n', m') $ then I will have irreducible representation. Let's say that I have $(1,1)\otimes(1,1)$. This decomposes to $$(1,1)\otimes(1,1)=(2, 2)\oplus(3,0)\oplus(0,3)\oplus(1,1)\oplus(1,1)\oplus(0,0) $$ and the dimension of each representation is respectively $$8\otimes8=27\oplus10\oplus{\bar{10}}\oplus8\oplus8\oplus1$$ because $$dim(n, m) =\frac{1}{2}(n+1)(m+1)(n+m+2) $$ In class we also did the decomposition with the Young Tableaux method(We worked on SU(3)).The result was this(12.14)

(Sorry for the inconvenience but I have been trying to upload the image and I cannot). My teacher then wrote above each diagram the tensor representation, which are just the same and in the same order as before. But the representation for (1,1) has two Young diagrams. My question is: Can we find a representation of a tensor that has two different young diagrams and is there a general rule that given a representation of a tensor $(n, m) $ we can write down its young tableaux? Also, I know how to decompose the direct product of two young diagrams and to find their multiplicity(dimension). Thanks. enter image description here

Assassinos
  • 79
  • What do you mean by the representation for (1,1) has 2 Young diagrams? – nobody Nov 19 '19 at 17:27
  • @justanothermathstudent i just uploaded the picture.That is what our teacher wrote in class. As you can see there are two different types of diagrams with (1,1). – Assassinos Nov 19 '19 at 19:28
  • The diagrams on the righthand side are obtained by starting from the first term in the product (in this case the partition (2,1)) and then adding boxes whose contents are determined by the second partition (in this case two a's and one b) with the property that the filling is semistandard and Yamanouchi: weakly increasing in rows, strictly down columns, and as you read by rows from right to left, at each point you have seen more a's than b's. I do not know what your notation $(m,n)$ means so I can't comment on the lefthand side. – Hugh Thomas Nov 20 '19 at 05:03
  • Essentially a duplicate of https://math.stackexchange.com/q/1525272/11127 – Qmechanic Jan 23 '25 at 11:54

0 Answers0