(I wasn't able to access the book you linked to, but I'm answering the question as posted.)
Consider the pentagon $N_5 = \{0,a,b,c,1\}$, with $0<a<b<1$, $0<c<1$ and $c$ incomparable to $a$ or $b$ (see it, for example, here), and define $\to$ by the table below.
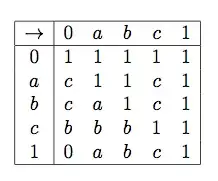
It is immediate that $x \to x = 1$, and it is not difficult to see that properties (2), (3) and (4) are satisfied as well.
For example, to verify (2), one has to check that the meet of the element on the head of each row with the element on the head of each column coincides with the the meet of the head of that row with the element in the cell that is the cross of that row and that column.
(3) is similar, but even easier.
To check (4), star by noticing that if $x\leq y$ then $x\to y=1$.
Thus, if $x\leq y$, (4) reduces to $x\to x = x \to y$, which is true since both are $1$;
if $x \geq y$, we get $x\to y = x \to y$, which is obvious;
if $x=1$, we get $1\to y = 1 \to y$;
and if $y=0$, we get $x \to 0 = x \to 0$.
So there are only four pairs $(x,y)$ to check: $(a,c),(b,c),(c,a),(c,b)$, and that is easy.
But this algebra doesn't satisfy property (0).
Indeed,
$$b\to(0\wedge a) = b\to 0 = c \neq
0 = c \wedge a = (b\to 0) \wedge (b\to a).$$
So this means that axiom (0) cannot be derived from axioms (1)—(4), and perhaps there is a wrong result in that book, as someone also suspected, in a comment.
