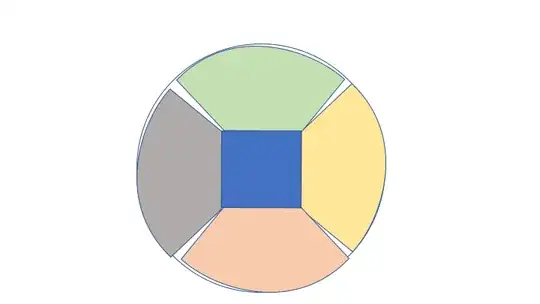
I'm having some problems understanding an exercise. The domain $\Omega$ is the unit circle. Then it says:
"To mesh it with quadrilateral elements, compose $\Omega$ from five mapped squares, one of them being a square centered at the origin. Propose five analytical mappings, one for each square."
How is that supposed to look like? Am I mapping a cross kinda thing into a circle? And why squares and not a triangular mesh? Where are the benefits to that?