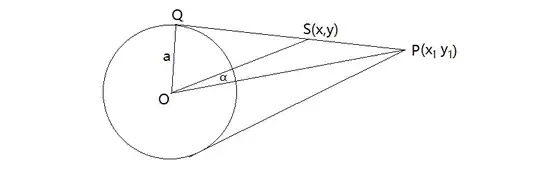
Pair of tangents drawn from a point $(x_1,y_1)$ to a circle $x^2+y^2=a^2$ is given by $$ SS_1=T^2\implies(x^2+y^2-a^2)(x_1^2+y_1^2-a^2)=(xx_1+yy_1-a^2)^2 $$
This is stated many where but most do not explain where does this come from. It is asked in a similar post The equation of a pair of tangents to a circle from a point, but is it possible to get an intuition into how the expression gives pair of tangents drawn from a point $(x_1,y_1)$ to a basic form of circle $x^2+y^2=a^2$ ?