Equation of non-axis-aligned ellipse resulting from hemisphere projected circle

Question

I've updated the title and information here because I'm not sure if my original question is mathematically correct.

This may be a duplicate of several questions on here, such as this one or this one. But even with them, I'm having some difficulty getting what I need.

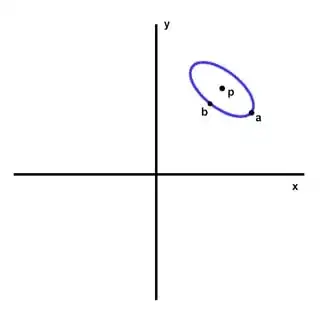
I'm doing some projecting of solid angles onto a 2D surface (image), and I need the equation of the resulting ellipse, to do pixel counting and point collision checks. I have the center point, and what I think is called a vertex and co-vertex? I don't have any focii.

Given a, b and p, I'm trying to find an equation for the blue ellipse that I can use for plotting and collision checks with pixels of an image. This is for science, not real-time graphics.

For context, here is an animation of some of the resulting ellipses. In theory I have a projected ellipse for every single integral polar coordinate (azimuth, altitude) [0-360, 0-90]. This animation was done with Grasshopper+Rhino, so I'm not plotting the ellipses from an equation.

Technically, the points I have come after a projection through a non-ideal (not perfectly linear) fisheye lens. So it's not an ideal hemisphere projection. So I can see having an issue finding the exact ellipse equation. In theory, I can project any number of points needed to find the ellipse. But, to be honest, getting it exact is not critical for this project, as an ideal projection and our projection vary slightly for the purposes of the bounds of this ellipse (the center point location and the radii are the most important).

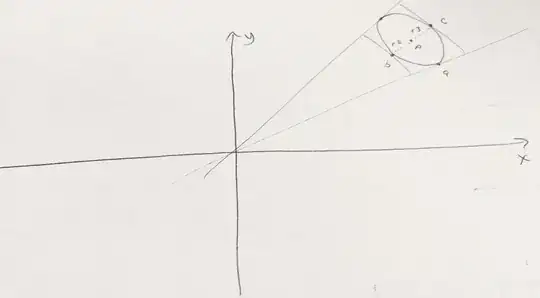
Update: I'm not entirely sure the result is always an ellipse after projection... Can someone confirm that? Looking at multiple points being projected, is it true that a circle projected would always result in an ellipse? Or is it possible for it to be an egg-shaped oval? For example, this is a very bad drawing, but is is possible for r3 to be greater than r2, or even if not, is it possible that points on the "bottom" half (furthest from origin) of the ellipse are not equally distant from the center point as the "top" half?

Answer 1

To check whether a point $x$ is inside the ellipse first compute vector $u = x - p$. Then project it onto the principal axes of the ellipse using dot products as follows:

$$ k = u . \frac{a-p}{||a-p||}\\ l= u . \frac{b-p}{||b-p||} $$

Then compute scaled sum of squares and compare with the cutoff:

$$ \frac{k^2}{||a-p||^2} + \frac{l^2}{||b-p||^2} > 1 $$

If you need an explicit equation of the ellipse you can plug in $u = (u_x,u_y)$ and follow the same procedure to get one.

Answer 2

EDIT.

The projection of a tilted circle on a plane is always an ellipse.

If you need a parametric equation for point $\vec r$ on the ellipse, than you can write it as: $$ \vec r=\vec p + (\vec a-\vec p)\cos t+(\vec b-\vec p)\sin t, $$ with $0\le t<2\pi$.

If you want the cartesian equation you can instead proceed as follows.

Let $\alpha=|\vec a-\vec p|$, $\beta=|\vec b-\vec p|$ and the equations of lines $ap$, $bp$ be $$ ax+by+c=0,\quad bx-ay+d=0 $$ respectively. If $A=(x,y)$ is any point on the ellipse, then its distances from lines $ap$ and $bp$ are respectively $$ AH={|ax+by+c|\over\sqrt{a^2+b^2}},\quad AK={|bx-ay+d|\over\sqrt{a^2+b^2}}. $$ The equation of the ellipse can be written as $AH^2/\alpha^2+BK^2/\beta^2=1$, that is: $$ {(ax+by+c)^2\over\alpha^2}+{(bx-ay+d)^2\over\beta^2}=a^2+b^2. $$

Answer 3

Let a plane say $x+y+z= 0.8 $ cut a unit radius sphere to make a small circle with latitude and longitude $\approx 45^{\circ}$ and view projection of this small (non-geodesic) intersected circle in plane of the prime meridian as an ellipse.