Boundary layer in time

Question

Consider the initial value problem $\varepsilon x'' + x' + tx = 0$ where $x(0) = 0$ and $x'(0) = 1$. I'm solving this problem using a matched asymptotic expansion. First, I let $$x(t, \varepsilon) = \varepsilon x_1(t) + \varepsilon^2 x_2(t) + o(\varepsilon^2),$$ and solve at corresponding orders of $\varepsilon$ and leave the coefficients undetermined. Then I define $T = t/\varepsilon$ and let $X(\varepsilon, T) = x(\varepsilon, t)$ and write the re-scaled equation $$X'' + X' + \varepsilon TX = 0.$$

Then solve this at the corresponding orders of $\varepsilon$ for the expansion $$X(\varepsilon, T) = \varepsilon X_1(T) + \varepsilon^2 X_2(T) + o(\varepsilon^3).$$ Assuming $X$ is my solution 'inside' the boundary layer, I let $X$ satisfy the initial conditions $X(0) = 0, X'(0) = \varepsilon$. Then $X_1(0) = 0, X_1'(0) = 1$ and $X_n(0) = 0, X_n'(0) = 0$ where $n>1$. However, when I solve for the solutions 'inside' the boundary layer I get imaginary error functions. I believe this will cause me problems later in the matching.

I believe I have solved this problem without the $t$ term and I am building up to a more complicated function. I am familiar with boundary laters in the context of space, but cannot find much on these 'initial layer' problems.

I know I have not provided my solutions here, but I want to know if my method is sensible or if someone knows a better method of solving this (equations of this type). I appreciate your response.

Answer 1

There appears to be a scale error in your re-balanced equation that might throw off later computations.

Perturbation series

Note: As $x''(0)=-ε^{-1}$, etc., the first terms of the Taylor expansion are $x-\frac12ε^{-1}x^2+O(x( ε^{-1}x)^2)$ which has a peak at $x=ε$ of magnitude $ε/2$. This means that simultaneously to rescaling the time, it makes sense to also scale to compensate the function so that the initial slope remains $1$.

With $X(T)=ε^{-1}x(εT)$ and thus $X'(T)=x'(εT)$, $X''(T)=εx''(εT)$ you should get $$ X''(T)+X'(T)=εx''(εT)+x'(εT)=-εTx(εT) \\ \implies X''(T)+X'(T)+ε^2TX(T)=0, ~~X(0)=0,~~X'(0)=1. $$ which means that the perturbation parameter is $ε^2$, $X(T)=X_0(T)+ε^2X_1(T)+ε^4X_2(T)+...$. The first order approximation is $X_0(T)=1-e^{-T}$. The next term is obtained via \begin{align} X_1''(T)+X_1'(T)&=-TX_0(T)=-T+Te^{-T}, ~~X_1(0)=0,~~X_1'(0)=0\\ X_1(T)&=-\tfrac12T^2-(\tfrac12T^2+T+1)e^{-T} \end{align} Further terms will have higher polynomial degrees, leading to divergence for $T\to \infty$ and thus no match to the outer solution.

However, knowing that the outer solution is $Ce^{-t^2/2}=Ce^{-ε^2T^2/2}=C(1-\frac12ε^2T^2+...)$, one can absorb the obvious terms of the perturbation expansion in similar terms \begin{align} X(T)=X_0(T)+ε^2X_1(T)+...&=1-\tfrac12T^2-(1+ε^2(\tfrac12T^2+T+1))e^{-T}+...\\ &=e^{-ε^2T^2/2}-e^{ε^2T^2/2}e^{-T} - ε^2(T+1)e^{-T} \end{align} or $$ x(t)=εe^{-t^2/2}-εe^{t^2/2}e^{-t/ε}-ε^2(t+ε)e^{-t/ε} $$ (or possibly also $x(t)=εe^{-t^2/2}-ε(2-e^{-t^2/2})e^{-t/ε}+...$, depending on the higher order terms)

But this is guess-work that could be invalidated with every new term in the perturbation series.

---

Two time-scale approach

Coming from a slightly different angle, starting from the inner solution, set the integration constants there directly as "slowly moving" functions of $t$, that is, try to find a two-scale solution as $$x(t)=εA(t)-εB(t)e^{-t/ε}.$$ Then immediately $A(0)=B(0)$. With the derivatives one finds the other initial condition and the insertion into the differential equation. \begin{align} x'(t)&=εA'(t)+(B(t)-εB'(t))e^{-t/ε}, \\ εx''(t)&=ε^2A''(t)-(B(t)-2εB'(t)+ε^2B''(t))e^{-t/ε}, \\ \hline 0=εx''(t)x'(t)+tx(t)&=ε[εA''(t)+A'(t)+tA(t)] - ε[-B'(t)+εB''(t)+tB(t)] e^{-t/ε},\\ 1&=ε(A'(0)-B'(0))+B(0). \end{align} In first order, separating the terms in $A$ and $B$ and using only the lowest order terms in $ε$, one finds the coefficients as $A_0(t)=e^{-t^2/2}$ and $B_0(t)=e^{t^2/2}$.

In the next order of $A(t)=A_0(t)+εA_1(t)$, $B(t)=B_0(t)+εB_1(t)$, $$ (e^{t^2/2}A_1(t))'=-(t^2-1)\implies A_1(t)=(t-\frac13t^3)e^{-t^2/2}\\ (e^{-t^2/2}B_1(t))'=(t^2+1)\implies B_1(t)=(t+\frac13t^3)e^{t^2/2} $$ so that $A'(0)=-ε$, $B'(0)=ε$, and again $A(0)=B(0)=1$

Plotting plots of these first and second order approximations against the numerical solution gives a good fit.

Answer 2

WKB approximation

Look for basis solutions of the form $x(t)=\exp(S(t)/ε)$. Then $εx'(t)=S'(t)\exp(S(t)/ε)$ and $ε^2x''(t)=[εS''(t)+S'(t)^2]\exp(S(t)/ε)$. Inserting and canceling the exponential gives $$ 0=e^{-S/ε}(ε^2x''+εx'+εtx)=εS''(t)+S'(t)^2+S'(t)+εt \\~~\\ \iff S'(t)^2+S'(t)=-ε(S''(t)+t). $$ For simplicity name $s(t)=S'(t)$ and compute the terms of the perturbation series $s(t)=s_0(t)+εs_1(t)+...$ \begin{array}{rlrl|rl} s_0^2+s_0&=0 &\implies s_0&=0 &\text{ or }~~ s_0&=-1\\ 2s_0s_1+s_1&=-t &\implies s_1&=-t & s_1&=t \\ s_1^2+2s_0s_2+s_2&=-s_1' &\implies s_2&=1-t^2 & s_2&=1+t^2\\ \end{array}

The approximation so far is $$ x(t)=A\exp(-\tfrac12t^2+ε(t-\tfrac13t^3))+B\exp(-ε^{-1}t+\tfrac12t^2+ε(t+\tfrac13t^3)) $$ with $0=x(0)=A+B$ and $1=x'(0)=-ε^{-1}B$, so that $A=ε$, $B=-ε$.

The plot of these two approximations against the numerical solution gives a good fit even for largish values of $ε$.

Answer 3

Using matched asymptotic expansions will lead to secular terms at $O(\epsilon^2)$. The $O(\epsilon)$ inner solution is $X_1(T)=1-e^{-T}$ and the outer solution is $x_1(t)=e^{-t^2/2}$. These give a uniform approximation $$x(t)=\epsilon\left(e^{-t^2/2}-e^{-t/\epsilon}\right)+O(\epsilon^2).$$ This approximation is actually quite good. Unfortunately however, the $O(\epsilon^2)$ terms contain secular terms and grow without bound.

To resolve this, use the method of multiple scales. Let $t_1=t$ and $t_2=\epsilon t$, then $x(t)=X(t_1,t_2)$. The equation for $X$ becomes (using subscripts to denote differentiation) $$ \epsilon X_{t_1t_1}+2X_{t_1t_2}+\frac{1}{\epsilon}X_{t_2t_2}+X_{t_1}+\frac{1}{\epsilon}X_{t_2}+t_1X=0, \quad X(0,0)=0,\quad X_{t_1}(0,0)+\frac{1}{\epsilon}X_{t_2}(0,0)=1.$$

Now let $X=X_0+\epsilon X_1+\ldots$, (see note 1) and then we get, at $O(\epsilon^{-1})$, $$X_{0,t_2t_2}+X_{0,t_2}=0,\quad X_0(0,0)=X_{0,t_2}(0,0)=0,$$ at $O(1)$, $$X_{1,t_2t_2}+X_{1,t_2}=-2X_{0,t_1t_2}-X_{0,t_1}-t_1X_0,\quad X_1(0,0)=0,\quad X_{1,t_2}(0,0)+X_{0,t_1}(0,0)=1,$$ and at $O(\epsilon)$, $$X_{2,t_2t_2}+X_{2,t_2}=-2X_{1,t_1t_2}-X_{1,t_1}-X_{0,t_1t_1}-t_1X_1,\quad X_2(0,0)=X_{2,t_2}(0,0)+X_{1,t_1}(0,0)=0.$$

Now, the solution of the $O(\epsilon^{-1})$ system is $$X_0(t_1,t_2) = A_0(t_1)e^{-t_2}+B_0(t_1)$$ where $A_0(0)+B_0(0)=0$ and $-A_0(0)=0$, so $A_0(0)=B_0(0)=0$.

The $O(1)$ equations are now $$X_{1,t_2t_2}+X_{1,t_2}=-2\left(-A_0'(t_1)e^{-t_2}\right)-A_0'(t_1)e^{-t_2}-B_0'(t_1)-t_1A_0(t_1)e^{-t_2}-t_1B_0(t_1),\quad X_1(0,0)=0,\quad X_{1,t_2}(0,0)+X_{0,t_1}(0,0)=1,$$ which simplifies to $X_{1,t_2t_2}+X_{1,t_2}=e^{-t_2}\left(A_0'(t_1)-t_1A_0(t_1)\right)-B_0'(t_1)-t_1B_0(t_1)$. To avoid secular terms we require $A_0'(t_1)-t_1A_0(t_1)=0$ and $B_0'(t_1)+t_1B_1(t_1)=0$ (see note 2). With the initial conditions we have, $A_0(0)=B_0(0)=0$, both $A_0$ and $B_0$ are $0$.

Now the $O(1)$ equations are nearly the same as the $O(\epsilon^{-1})$ equations: $$X_{1,t_2t_2}+X_{1,t_2}=0,\quad X_1(0,0)=0,\quad X_{1,t_2}(0,0)=1,$$ except for the initial condition. The solution of this system is $$X_1(t_1,t_2) = A_1(t_1)e^{-t_2}+B_1(t_1)$$ where $A_1(0)+B_1(0)=0$ and $-A_1(0)=1$. So $A_1(0)=-1$ and $B_1(0)=1$. The $O(\epsilon)$ equation is then $$X_{2,t_2t_2}+X_{2,t_2}=A_1'(t_1)e^{-t_2}-B_1'(t_1)-t_1A_1(t_1)e^{-t_2}-t_1B_1(t_1),\quad X_2(0,0)=0,\quad X_{2,t_2}(0,0)+A_1'(0)+B_1'(0)=0.$$ Again, to avoid secular terms we need $A_1'(t_1)-t_1A_1(t_1)=0$ and $B_1'(t_1)+t_1B_1(t_1)=0$. So $A_1(t_1)=ce^{t_1^2/2}$ and $B_1(t_1)=de^{-t_1^2/2}$, and the initial conditions give $c=-1$ and $d=1$.

We now have a full expression for $X_1$, so $$ X_1(t_1,t_2)\approx-e^{t_1^2/2}e^{-t_2}+e^{-t_1^2/2},$$ or, in terms of $x$ and $t$, $$ x(t)=\epsilon \left(e^{-t^2/2}-e^{t^2/2}e^{-t/\epsilon}\right)+O(\epsilon^2). $$

This is very similar to the matched asymptotics result above, but it can be continued to get higher-order approximations. For example, $$x(t)=\epsilon \left(e^{-t^2/2}-e^{t^2/2}e^{-t/\epsilon}\right)+\epsilon^2 e^{-t^2/2}\left(t-\frac{t^3}{3}\right)\left(1-e^{-t/\epsilon}\right)+O(\epsilon^3). $$

Note the growing term $e^{t^2/2-t/\epsilon}$ which grows with time. This is incorrect behaviour so the approximation is valid for early times.

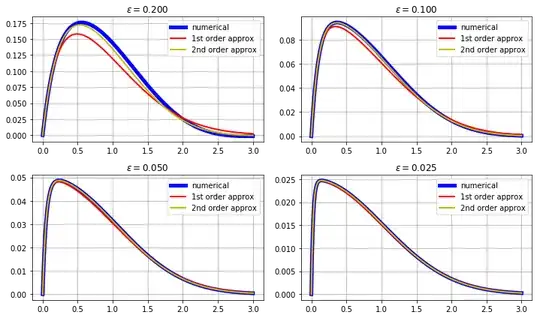
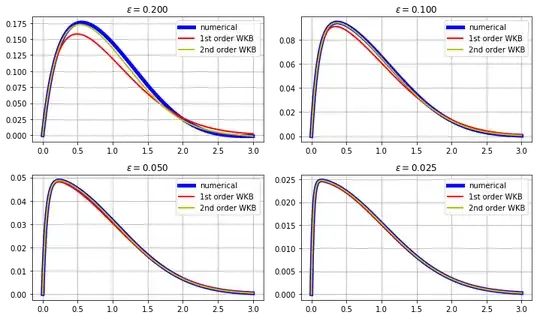
Results with $\epsilon=0.2$. Shown are a numerical solution, the inner and outer solutions for the leading-order matched asymptotics and corresponding uniform approximation, and both of the multiple-scales results (ms1 and ms2). Note the very good agreement with the two-term multiple-scales expression and the numerical result.

---

Note 1: We don't need to include $X_0$ since it will be zero, but I left it in for generality, and because I'm not sure if it's obvious that it will be zero.

Note 2: There's actually no real justification to remove terms that lead to things like $t_2e^{-t_2}$, but it is usually done, and it works.

Answer 4

This is not an answer to the question, but I think it might be useful nevertheless.

This equation can be solved exactly in terms of Airy functions. Let $x(t)=e^{\lambda t}W(t)$ and substitute into the differential equation to give (after factoring out $e^{\lambda t}$, $$\epsilon\lambda^2 W(t)+2\epsilon\lambda W'(t)+\epsilon W''(t)+\lambda W(t)+W'(t)+tW(t)=0. $$ If $2\epsilon\lambda+1=0$ then we can remove the $W'$ terms, so $\lambda=-1/(2\epsilon)$ and $u=e^{-t/(2\epsilon)}$. This represents the slow decay in the solution for $x(t)$.

Now we are left with $$\frac{1}{4\epsilon} W+\epsilon W''-\frac{1}{2\epsilon}W+tW=0\Rightarrow \epsilon^2 W''+\left(\epsilon t-\frac{1}{4}\right)W=0.$$

The initial conditions are, in terms of $W$, $W(0)=0$ and $W'(0)=1$. Now let $$s=\frac{1-4\epsilon t}{4\epsilon^{4/3}}$$ and $H(s)=W(t)$ so that $ H'(s)=-W'(t)\epsilon^{-1/3}$ and $H''(s)=\epsilon^{-2/3}W''(t)$. Then $$H''(s)-sH(s)=0,\quad H\left(\frac{1}{4\epsilon^{4/3}}\right)=0,\quad H'\left(\frac{1}{4\epsilon^{4/3}}\right)=-\epsilon^{1/3}.$$

This is the Airy differential equation, and its solution is a combination of Airy functions $\textrm{Ai}(s)$ and $\textrm{Bi}(s)$, $$ H(s) = c_1\textrm{Ai}(s)+c_2\textrm{Bi}(s),$$ and $c_1$ and $c_2$ satisfy $$ c_1\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)+c_2\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)=0,\quad c_1\textrm{Ai}'\left(\frac{1}{4\epsilon^{4/3}}\right)+c_2\textrm{Ai}'\left(\frac{1}{4\epsilon^{4/3}}\right)=-\epsilon^{1/3}, $$ or $$c_1 = \epsilon^{1/3}\frac{-\textrm{Bi}\left(\frac{1}{4\epsilon^{4/3}}\right)}{\left(\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Bi}'\left(\frac{1}{4\epsilon^{4/3}}\right)-\textrm{Ai}'\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Bi}\left(\frac{1}{4\epsilon^{4/3}}\right)\right)},$$ and $$c_2 = -\frac{\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)}{\textrm{Bi}\left(\frac{1}{4\epsilon^{4/3}}\right)} $$ Calculating these values of the Airy functions and their derivatives is not necessarily simple.

Substituting back for $W$ gives $$ W(t) = c_1\textrm{Ai}\left(\frac{1-4\epsilon t}{4\epsilon^{4/3}}\right)+c_2\textrm{Bi}\left(\frac{1-4\epsilon t}{4\epsilon^{4/3}}\right) $$ and so $$x(t) = \frac{\epsilon^{1/3}e^{-t/(2\epsilon)}\left[-\textrm{Bi}\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Ai}\left(\frac{1-4\epsilon t}{4\epsilon^{4/3}}\right)+\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Bi}\left(\frac{1-4\epsilon t}{4\epsilon^{4/3}}\right)\right]}{\textrm{Ai}\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Bi}'\left(\frac{1}{4\epsilon^{4/3}}\right)-\textrm{Ai}'\left(\frac{1}{4\epsilon^{4/3}}\right)\textrm{Bi}\left(\frac{1}{4\epsilon^{4/3}}\right)}. $$

I do think WKB theory is necessary for the asymptotics (especially if you replace $t$ by $\cos(t)$), and for the equation in terms of $W$ there will be three regions, one where $1/4-\epsilon t>0$, one where it is negative, and a connection region where it is small. The book "Introduction to perturbation methods" by Mark Holmes has a good section on WKB problems with turning points.