Homotopy equivalence between spaces intuition

Question

Before this is marked as a duplicate, I have already went through all similar titled threads and none were helpful for the confusion I'm having, which I will explain shortly.

Two spaces $X$ and $Y$ are homotopy equivalent if there are continuous functions $f$ and $g$ such that $f:X \to Y,g: Y \to X$ such that $g \circ f$ and $f \circ g$ are both homotopic to the identity.

What I want to understand is what intuitive idea this definition captures and why that idea follows from the definition. All threads I've seen that address this question only address the former and not the latter.

Here is what I mean by this. These threads usually are something to the effect of "Homotopy equivalent spaces can be thought of as spaces that can be continuously stretched, squished, deformed into the other" without explaining how this intuitive sentiment is translated from the formal definition. If not, these threads will try to make the idea of a homotopy intuitive through the use of various examples, usually deformation retractions.

Here are some examples of these threads: 1, 2, this one, I don't have the background to fully understand, 4, Wikipedia, and a lot more.

I understand the idea behind a homotopy and I intuitively understand how a deformation retraction looks like. Indeed, I understand that a deformation retraction satisfies the definition of homotopy equivalence - but that's just it. I know how to show it satisfies the property of homotopy equivalence, just like I know that integer addition satisfies associativity. But why should I believe that the homotopy equivalence definition captures the intuitive idea that people claim it captures when associativity of a binary operator doesn't fully capture the idea addition? It feels arbitrary.

In conclusion, Homotopy equivalence seems like an arbitrary weakening of the homeomorphism definition and I can't seem to divine any intuition from its formal definition. I've scoured the internet and multiple texts and none were helpful. This is a problem as I try to proceed through Hatcher without any intuition of it whatsoever.

Answer 1

Let's try to see (purely formally) that homotopy equivalence is the right notion of equivalence for what we are studying. When doing mathematics, we are often interested in how objects behave up to some notion of isomorphism. The standard notion of isomorphism in a topological space is that of a homeomorphism, but this turns out to be too restrictive. While homeomorphism preserves ALL the topological data of a space, we are only interested in preserving the topological data which we can detect with certain methods.

As a crude example, let's say that we're only interested in studying the homology of a space. Here homeomorphism is clearly not the right notion of equivalence, because there are lots of spaces which look the same as far as homology is concerned, but which are not homeomorphic. Can we find a better notion of equivalence?

---

You say in the comments that you're happy with the notion of a homotopy between paths. This is a way of saying that two paths are equivalent, so maybe we can beef it up to show that two spaces are equivalent in a similar way.

Say $f, g : I \to A$ are paths from $a$ to $b$.

(That is, $I = [0,1]$ is the unit interval, $f(0) = g(0) = a$ and $f(1) = g(1) = b$)

We say they are homotopy equivalent if there is a function $H : I^2 \to A$ with $H(x,0) = f(x)$ and $H(x,1) = g(x)$. The picture, which I'm sure you're familiar with, is shown below (shamelessly stolen from this website):

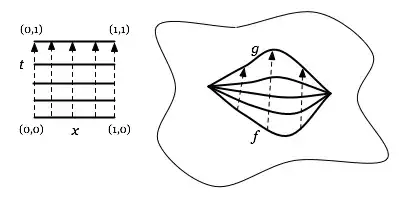
Intuitively, we can "fill the space" bounded by $f$ and $g$ with a copy of the unit square $I^2$.

---

Ok, let's beef this definition up one step at a time. A path is just a function, so maybe we can find some way of viewing functions as equivalent in a way that extends the definition of path equivalence.

Well, let's say that $f, g : A \to B$. How might we view them as equivalent? Why not do the same thing? Say $H : A \times I \to B$ is a homotopy connecting $f$ and $g$ iff $H(a,0) = f(a)$ and $H(a,1) = g(a)$.

If we fix $a$, then we are saying that $H(a,t)$ gives a path between $f(a)$ and $g(a)$, which clearly generalizes our old notion of equivalence of paths!

---

Ok, so we have some way of viewing functions as "the same", because there is a way to connect the outputs in such a way that we can "deform" $f$ into $g$ (by moving each point along the homotopy $H$). Does this notion of function equivalence actually buy us anything?

Yes! Recall we are only interested in homology, and we know that $f : A \to B$ induces a map $f_* : H_n(A) \to H_n(B)$. It isn't hard to show that if $f$ and $g$ are homotopic, then $f_* = g_*$! Notice I'm not saying the induced maps are homotopic, I'm saying the induced maps are the same.

Now it's not hard to see that $id_A : A \to A$ satisfies $(id_A)_* = id_{H_n(A)}$. It takes a little bit more work to see that if $f : A \to B$ and $g : B \to C$, then $(g \circ f)_* = g_* \circ f_*$. Both of these points have been shown countless times on MSE, so I won't bother showing them here.

---

Of course, with this under our belt, the definition of homotopy equivalence falls into our lap! If we want to know that $A$ and $B$ have the same homology, then we need to show that $H_n(A) \cong H_n(B)$.

So we want to consider $A$ and $B$ equivalent if some $f : A \to B$ induces $f_*$ an isomorphism between $H_n(A)$ and $H_n(B)$.

So $f_*$ should have an inverse $g_*$ such that $f_* \circ g_* = id_{H_n(B)}$ and $g_* \circ f_* = id_{H_n(A)}$. But we know how to guarantee this!

By the two properties above, it is enough to show that $f \circ g$ is homotopic to $id_B$ and $g \circ f$ is homotopic to $id_A$! This is exactly the notion of a homotopy equivalence between $A$ and $B$!

---

Ok, so homotopy equivalence is enough, but why is it better than homeomorphism? The answer is because it makes computations easier. It is much easier to show that two spaces are homotopy equivalent than to show they are homeomorphic, and with this new (weaker) notion of equivalence, we can compare the homology of spaces that aren't homeomorphic. I.e. $R^n$ is homotopic to a point, and it is easy to see that a point has trivial homology. If we insisted on using homeomorphism as our notion of isomorphism, we would not be able to make this comparison, and we would have to re-compute the homology of $R^n$ (or use homotopy equivalence as a theorem all over the place, which is basically what we're doing anyways, we're just honest about the fact that it's all we care about, so we take it as a definition of equivalence).

---

So we see now that, in our quest to have a weak (and therefore useful) notion of equivalence of spaces, we have quickly found our way to the notion of a homotopy equivalence. What is perhaps more surprising is that this same notion of equivalence falls out, whether we are trying to be invariant under homology, or under many of the countless other constructions in algebraic topology.

This is what makes the definition seem its most natural to me personally. The fact that trying to preserve a variety of different constructions always gives rise to the same notion of equivalence shows that we are onto something which is important. It is the farthest thing from arbitrary I can think of.

---

I hope this helps ^_^

Answer 2

If you find identifying homotopic maps motivated, I claim that you have to study spaces up to homotopy equivalence!

It is a common exercise to verify that taking homotopy classes interacts well with composition of functions. Hence, there is a category which has its objects topological spaces and its morphisms the homotopy classes of maps between spaces. (If you don't find looking at this category motivated, note that when we take the basepointed version of this category, the fundamental group of $(X,x_0)$ is exactly the set of morphisms from $(S_1,1)$ to $(X,x_0)$.)

When we have a category, it makes sense to study the objects of the category up to isomorphism. So what are the isomorphisms in this category? Well an isomorphism is a morphism that has left and right inverses. So to talk about left and right inverses we need to know what the identity morphism is. This is exactly the class of maps homotopic to the identity. And if you spell the rest of this stuff out, you will see the isomorphisms here are exactly the homotopy equivalences.

Another way to define the homotopy equivalences is by declaring a map $f:X \rightarrow Y$ to be a homotopy equivalence if precomposition with $f$ (which is well defined) gives a bijection $[Y,Z] \rightarrow [X,Z]$ and postcomposition gives a bijection $[W,X] \rightarrow [W,Y]$ for all $W,Z$ where $[-,-]$ denotes homotopy classes of maps.

Answer 3

"These threads usually are something to the effect of "Homotopy equivalent spaces can be thought of as spaces that can be continuously stretched, squished, deformed into the other" without explaining how this intuitive sentiment is translated from the formal definition."

Let's see if this helps understanding the intuition behind the definition.

First let's consider deformation retracts:

$A \subset X$ is a deformation retract of $X$ if there exists $r:X \rightarrow A$ such that $i \circ r $ is homotopic to $Id_X$.

Now consider the two dimensional disc $X=D^2$ and the point $x_0=(0,0)\in X$. Then the map $f(t,x)=x_0$ transforms the identity $Id_X$ to the constant function $\epsilon_0:X \rightarrow \{x_0\}$ such that under the map $f$, but the deformation is not continuous respect time.

This is, if you consider $f: I \times X \rightarrow X$ taking place in a time $t\in [0,1]$, then $f$ inmediately transforms $Id(x)=x$ into $i \circ \epsilon_0(x)=x_0$ in $t=0$ and then it stays the same for the rest of the period $0<t \leq 1$. So, in other words, it doesn't hold that for times $t_0, t_1 \in [0,1]$ very close between each other the functions $f_{t_0}$ and $f_{t_1}$ look very similar form each other.

On the other hand, the map $g: I \times X \rightarrow X$ such that $g(t,x)=(1-t)x + tx_0$ does the required deformation continuously with respect time, so $g$ is an homotopy between $Id_X$ and the constant map $i \circ \epsilon_0$ and therefore $\{x_0\}$ is a deformation retract of $D$.

And that is precisely where the definition of deformation retract comes into play. The transformation $g$ between $Id_X$ and $i \circ \epsilon_0$ being an homotopy means that the shrinking that it performs is continuous with respect to the time $t$, while the map $f$ is not an homotopy and therefore the shrinking has not been performed continuously with respect time.

And homotopy equivalences are basically a more general notion than deformation retracts, this is, instead of having $X$ and $A\subset X$ we have $X$ and $Y$ arbitrary, and instead of the inclusion $i$ we have a continuous map $g:Y\rightarrow X$.

"In conclusion, Homotopy equivalence seems like an arbitrary weakening of the homeomorphism definition and I can't seem to divine any intuition from its formal definition."

If you keep reading Hatcher you'll find out about fundamental groups, and you'll learn that homotopy equivalent spaces have isomorphic fundamental groups, which is very nice since being homotopy equivalent is a weak condition compared, for example, with being homeomorphic.