4

The problem sounds easy, that is, if I would have had an easy function $\phi(k_p, k_i, \omega)$ that defines these ellipses. This function, $\phi$ depends on which transfer system $G(s)$ I am trying to design a controller for. For example if I take $$ G_1 (s) = \frac{1}{(s+1)^3}$$ the function is defined as:

$$\phi(k_p,k_i,\omega) = \frac{1}{(\omega^2+1)^3} \cdot \Big(k_p^2 + (2-6\omega^2)k_p + \frac{k_i^2}{\omega^2} + (2\omega^2 - 6)k_i \Big) + \frac{3}{4}$$

(I don't think it's necessary that I explain why the function is defined like this. If it is, I'll explain that as well).

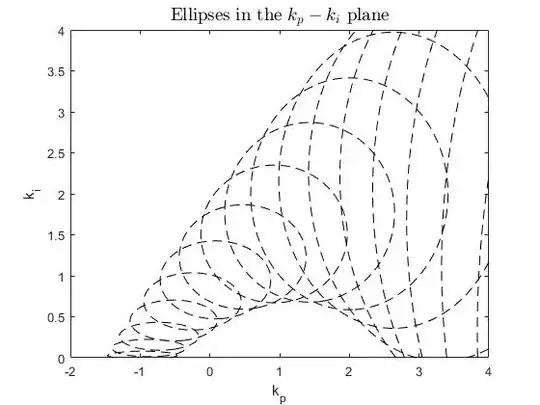
When I compute for $\omega = 0:0.1:5$ in $\phi$ I get 50 ellipses and the inside envelope is described by a hyperbole*(for this particular system). I have to find the equation of that hyperbole and its maximum.

enter image description here

Now I have tried 2 ways of solving this problem.

The easy way to find an approximate function of the envelope is to pick 5 points on the family of ellipses that the function will go through. I got a pretty good estimate but this has two downsides: I have to pick those points manually, so I can not automate this process in matlab. And it is an approximate function, so I will not find the best values for $k_p$ and $k_i$ for a certain $\omega$. See image below for results.

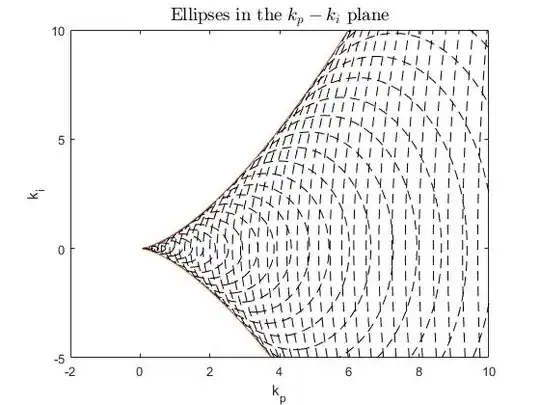
enter image description here

I also tried to solve this analytically, but that only worked for a simple system, such as $$G_2 (s) = \frac{1}{s^2}$$ This can in fact be solved analytically with matlab's symbolic toolbox and I get a function for the envelope. But for $G_1$, as mentioned above, I get expressions for $\omega$ that are not usable for the analytical method. The expressions contain roots and when substituting this in $\phi$ matlab sort of trips.
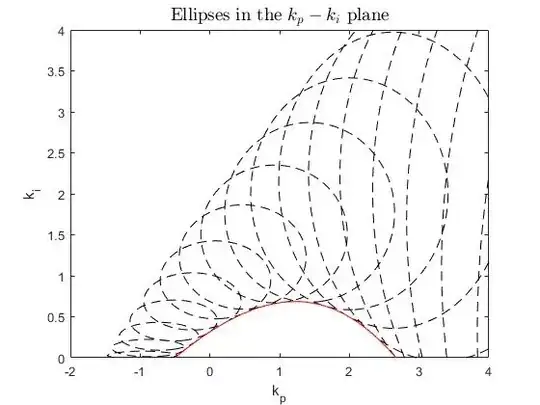
The method is simply taking the derivative of $\phi(k_p,k_i,\omega)$ w.r.t. $\omega$, then isolate $\omega$ and finally substitute the $\omega$ found in $\phi(k_p,k_i,\omega)$. $\phi$ is only dependent on $k_p$ and $k_i$ and it will give the envelope of the ellipses. ( used this site) See results below in the image.

enter image description here

So my question is: how do I find the (inside) envelope of these ellipses defined by $\phi(k_p,k_i,w)$, $\omega$ being the parameter of the ellipses?

Do I have to look for the points analytically? Or can I do it some other way? I am really out of ideas.

If there is something missing or my question is not clear, I would gladly explain more.

*I said the envelope was an ellipse, but it was a hyperbole

Paperreader
  • 45
  • In the third figure, it doesn't at all look like the envelope is another ellipse. Are you sure the envelope is always an ellipse? Nice problem, by the way! +1 – Adrian Keister Sep 03 '19 at 15:43
  • Well, if it helps, your problem seems to me to be analogous to the problem of finding a convex hull. Problem is, of course, your "hull" isn't always convex, so some of the methods used in finding convex hulls might not apply. – Adrian Keister Sep 03 '19 at 15:57
  • Thank you for your reply, I will try to see if I can use that approach. – Paperreader Sep 03 '19 at 16:01
  • The first figure can maybe deleted. – Narasimham Sep 04 '19 at 06:13
  • Are you sure your corrected equation is the right one? Th figure I get is very different from yours. – Intelligenti pauca Sep 04 '19 at 10:23
  • This is the exact output I get in matlab, without simplifying anything: $$\phi = x^2/(w^2 + 1)^3 - (2x(3w^2 - 1))/(w^2 + 1)^3 + (2y(w^2 - 3))/(w^2 + 1)^3 + y^2/(w^2(w^2 + 1)^3) + 3/4$$ – Paperreader Sep 04 '19 at 10:35
  • You must correct the front factor to $1/(1+w^2)^3$. – Intelligenti pauca Sep 04 '19 at 10:47
  • thank you very much, I missed that! Sorry for the mistakes. – Paperreader Sep 04 '19 at 10:58
  • The envelope is not a hyperbola. Eliminating $\omega$ from the system $$\phi(k_p, k_i, \omega) = 0, \ \frac \partial {\partial \omega} \phi(k_p, k_i, \omega) = 0$$ gives a degree 8 polynomial which is irreducible over the reals. The highest point is $(k_p, k_i)$ s.t. $$16 k_p^3 - 168 k_p^2 + 21 k_p + 196 = 0, \ 1024 k_i^3 - 8064 k_i^2 + 4887 k_i + 108 = 0.$$ – Maxim Sep 04 '19 at 20:52
  • Maxim, I took another look at the envelope I found. It is only a good approximation in the region of interest (because I picked 5 points in that region). When I zoom out, I find that it is indeed not the envelope of the ellipses. Thanks! – Paperreader Sep 05 '19 at 06:21
  • @Paperreader Are you interested in approximating the envelope only on some interval? – Intelligenti pauca Sep 05 '19 at 08:39
  • I would like to have the envelope for all $\omega \in [0, \infty)$. – Paperreader Sep 05 '19 at 08:46

0 Answers0