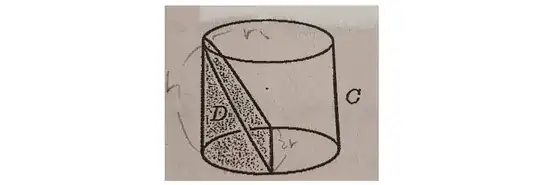
Let $C$ be a solid cylinder with the height $h$ and whose base is a circle of radius $r$. And let $D$ be the result of slicing $C$ by a plane whose intersection with on base circle is a point and whose intersection with the other base circle is a diameter. Then I have to calculate the volume of $D$. A crude picture is as below
I think the voluem of $D$ is gained by accumulating the volume of each left half-disk of radius $r(1-x/h)$ with the infinitesimal height $dx$, where $x$ ranges from $0$ to $h$. As a result, the answer is
$$\int_0^hr^2(1-x/h)^2(\pi/2)dx=\pi r^2h/6.$$
Is my argument correct? Could anyone please explain more persuasively that the sliced bases at height $x$ forms a half-disk of radius $r(1-x/h)$?