2

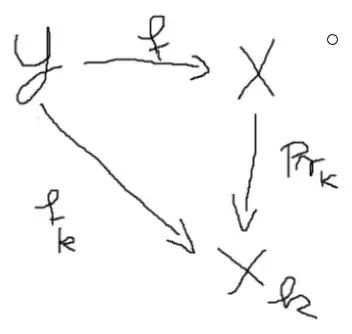
Let $(X_j, \tau_j)_{j\in J}$ be a family of topological spaces. Let $X=\prod_{j\in J} X_j$ provided with the product topology and let $pr_k: X\to X_k$ be the projection on the $k$-th coordinate, then has $(X,\tau, (pr_j)_{j\in J})$ the following universal property:

Is $Y$ a topological space $(f_j: Y\to X_j)_{j\in J}$ a familiy of continuous functions, then there is exactly one continuous function $f:Y\to X$ such that for every $k$ holds $f_k=pr_k\circ f$

enter image description here

This universal property of $X$ and the function $pr_k$ characterizes $(X,\tau, (pr_j)_{j\in J})$ unique up to homeomorphism.

I have a question why this characterizes up to homeomorphism.

The proof goes as follows:

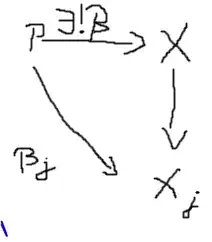
Suppose $P$ is a topological space with functions $\beta_j: P\to X_j$ which has the same universal property. With that we get:

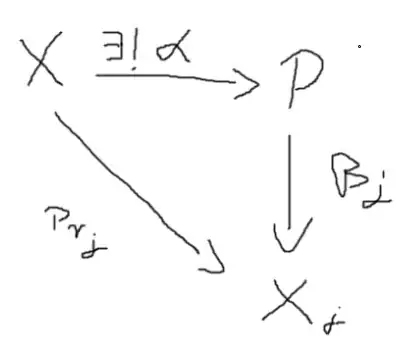
enter image description here enter image description here

Now observe $\alpha\circ \beta: P\to P$ (Note that the $X$ in the following picture is supposed to be $P$)

enter image description here

Then $\alpha\circ\beta =\operatorname{id}_P$, because of $\alpha$ and $\beta$ beeing unique.

Similarly $\beta\circ\alpha = \operatorname{id}_X$ so $\alpha$ and $\beta$ are homeomorphic.

My question:

Why is $\alpha\circ\beta=\operatorname{id}_P$. And what has the uniqueness to do with it?

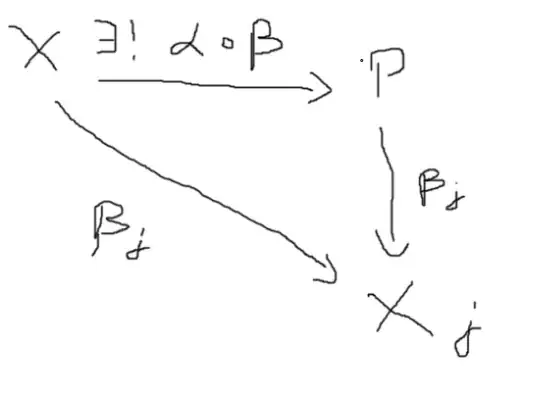
From the diagramm in the last picture we get that

$\beta_j\circ(\alpha\circ\beta)=\beta_j$ which implies $\alpha\circ\beta=\operatorname{id}_P$ immediatly.

Since $\beta_j\circ (\alpha\circ\beta(p))=\beta_j(p)\Leftrightarrow \alpha\circ\beta(p)=p$ for every $p\in P\Leftrightarrow \alpha\circ\beta=\operatorname{id}_P$.

What has the uniqueness to do with it?

Thanks in advance and excuse me for these awful images, but creating such diagrams on this website is always an odysse on its own...

Community
  • 1
Cornman
  • 11,370
  • 5
  • 35
  • 68
  • 1
    Note that both $\alpha\circ\beta$ and $\mathrm{id}_{P}$ “fit” into the corresponding diagram. The uniqueness clause of the universal property tells you that since both maps “work”, but the map that works is unique, the two maps must actually be the same map, so that $\alpha\circ \beta$ equals $\mathrm{id}_P$. By the way: it is false that if $h\circ f = f$ then $h$ must be the identity map. – Arturo Magidin Aug 20 '19 at 03:52
  • You mean $h\circ f = h$, dont you? Thanks for your comment. That answers my question. – Cornman Aug 20 '19 at 03:55
  • 2
    Either one. $h\circ f = h$ does not imply $f=\mathrm{id}$, and $h\circ f = f$ does not imply $h=\mathrm{id}$. At least not by itself. – Arturo Magidin Aug 20 '19 at 04:13
  • 1
    By the way, there is nothing “topological” about this proof. This is the standard categorical proof that an object that has the categorical property of being a “product” is unique up to unique isomorphism. – Arturo Magidin Aug 20 '19 at 05:10
  • @ArturoMagidin Interesting. I barly know anything about category theorie yet. – Cornman Aug 20 '19 at 05:48

1 Answers1

3

You know that $\alpha: X \to P$ satisfies $$\forall j: \beta_j \circ \alpha = \text{pr}_j\tag{1}$$

and $\beta: P \to X$ satisfies $$\forall j : \text{pr}_j \circ \beta= \beta_j \tag{2}$$

now using $(1)$ and $(2)$ we get that for any $j$:

$$\text{pr}_j \circ (\beta \circ \alpha) = (\text{pr}_j \circ \beta) \circ \alpha = \beta_j \circ \alpha = \text{pr}_j\tag{3}$$

And in the diagram we get from applying the universal property for $X$ to the test space $X$ itself, we are promised a unique $\gamma: X \to X$ such that

$$\forall j: \text{pr}_j \circ \gamma = \text{pr}_j\tag{4}$$

Now, $(3)$ tells us that $\gamma = \beta \circ \alpha$ also obeys $(4)$ and standard common sense (or the axioms of a category, in a more abstract setting) tells us that $\gamma=\text{id}_X$ also satisfies $(4)$.

So the unicity of $\gamma$ tells us $\beta \circ \alpha = \gamma = \text{id}_X$ and in particular, $$\beta \circ \alpha = \text{id}_X$$

The $\alpha \circ \beta = \text{id}_P$ follows similarly from applying the universal property of $P$ to $P$ and a similar small computation to $(3)$.

Henno Brandsma
  • 250,824