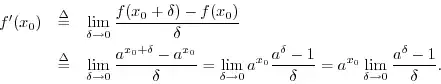2

Reading this page to understand where does Euler's Theorem come from, the proof gets to a point where it tries to define the derivative of the exponent functions $f(x) = a^x$ as follows:

First it states that

enter image description here

Next it notes that, given

$$\lim_{\delta\to0}\frac{2^\delta-1}{\delta}<1<\lim_{\delta\to0}\frac{3^\delta-1}{\delta}\ ,$$

there must be an $a$ such that $\lim_{\delta\to0}\frac{a^\delta-1}{\delta} = 1$ and this $a$ is defined to be a number $e$.

Now, I get why there must be such $e$ given this last fact, but how to prove this fact non circularly? To evaluate those limits one would use l'Hospital's rule, hence deriving an exponential function, which is precisely what we are trying to define.

Is there another way of evaluating these limits without deriving the exponentials $2^\delta$ and $3^\delta$?

Albert
  • 747
  • These limits are exactly the definitions of the derivatives of the exponential functions at $\delta=0$. You are asking if you can find the derivatives without deriving the exponentials? – Peter Foreman Aug 18 '19 at 14:58
  • Not exactly. I'm asking if I can define the derivative of the exponential function through these limits, but evaluating these limits without l'Hospital's rule, since for the case applying this rule implies deriving an exponential. The reasoning seems circular. Am I wrong? – Albert Aug 18 '19 at 15:07
  • 2
    There are many ways in which we can find this limit without L'Hôpital's rule (which is a circular method). See this question. – Peter Foreman Aug 18 '19 at 15:17
  • That's what I meant, @PeterForeman. Thank you. – Albert Aug 18 '19 at 15:29

0 Answers0