$\psi- \theta$ relation in Conics

Question

Angles $(\psi -\theta) $ relation is unique for Conics in a 3D situation.

// It is to seek $r- \psi$ of planar sections aka Conics on Gauss curvature $K=0$ cones for uniqueness and generality. Motivation/Background is mentioned although not absolutely necessary for the question at present. It needed mentioning due to the simplicity of their relationship in deeper contexts.

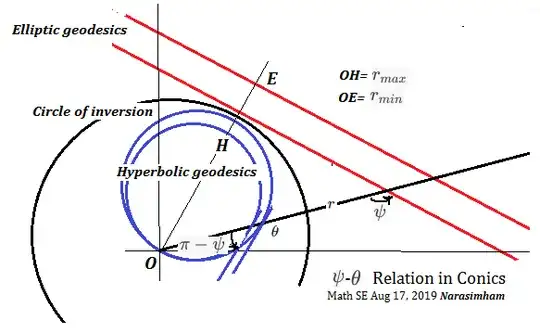
Angle $\psi $ is reckoned counterclockwise direction consistently from radius vector to one of parallel geodesics. Constant rotation $\phi$ and curvature in two dimensions shown here:

Elliptic geometry

$$ \phi_{Elliptic}= \psi +\theta = const $$ Differentiating with respect to arc for elliptic straight lines $$ \psi^{'}+\frac{d\theta}{ds} = \psi^{'}+\frac{\sin \psi}{r} =\kappa_{gElliptic}=0$$ Re-integrate we get Clairaut's constant in polar coordinates: $$ r\cdot \sin \psi = r_{min} = OE $$

By Inversion

the angle $\psi$ remains constant in magnitude but changes sense/relative direction into

Hyperbolic geometry

$$ \phi_{Hyperbolic}= (\pi-\psi ) +\theta = const $$ Differentiating with respect to arc for hyperbolic straight lines

$$ \psi^{'}-\frac{d\theta}{ds} =\psi^{'}-\frac{\sin \psi}{r} =\kappa_{gHyperbolic} =0$$

Re-integrate we get constant ; $$ r/\sin \psi = r_{max} = OH $$

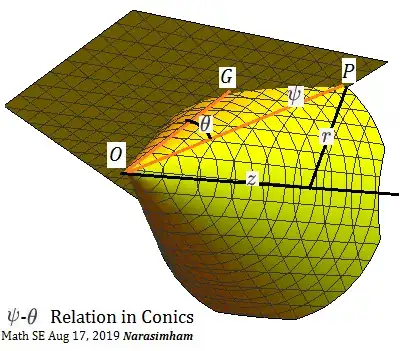
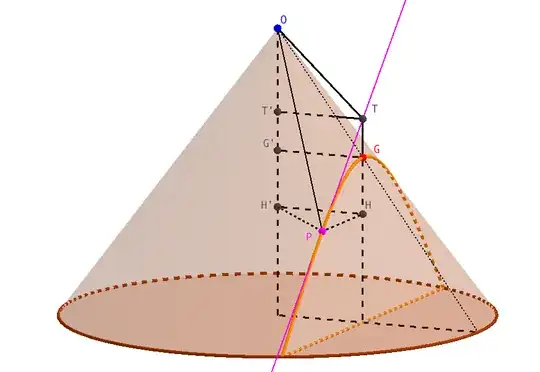
$ (r, \theta, z) $ are cylindrical coordinates and tangent at $P$ to conic makes angle $\psi $ to cone generator $OP$ to compare in this form their projections with elliptic and hyperbolic geodesics in two dimensions. //

If it is constant for example when $ \psi = \pi/2 \text{ at } G $ then we have a circle formed by cutting a cone of any semi-vertical angle with a plane perpendicular to the cone axis.

How to establish/ find this relation?

Thanks for help in finding a reference or hints.

Answer 1

It's not really clear what kind of relation OP expects, but here's something ...

Let the generators of a cone (with vertex at the origin and $z$-axis as axis) make angle $\alpha$ with the $xy$-plane. Let a cutting plane parallel to the $y$-axis make angle $\beta$ with the $xy$-plane, and let it meet the cone at $V := (-v \cos\alpha,0,v \sin\alpha)$ (which will be a vertex of the conic). That is, the cone and plane have equations $$z^2 \cos^2\alpha = (x^2+y^2)\sin^2\alpha \qquad\qquad (x+v\cos\alpha)\sin\beta=(z-v\sin\alpha)\cos\beta$$ We can parameterize the intersection of the plane and cone by $$P := p (\cos\alpha \cos\theta, \cos\alpha\sin\theta,\sin\alpha)$$ with $\theta$-dependent $p$ determined by substituting $P$ into the plane equation. The fully-parametric form of $P$ is then
$$P = \frac{v \sin(\alpha+\beta)}{\sin\alpha\cos\beta - \cos\alpha\sin\beta \cos\theta}\,(\cos\alpha \cos\theta, \cos\alpha\sin\theta,\sin\alpha)$$ A tangent vector $P'$ is proportional to the derivative of $P$ with respect to $\theta$; in particular, we can take $$P' = ( \sin\alpha\cos\beta\sin\theta, \cos\alpha\sin\beta-\sin\alpha\cos\beta\cos\theta, \sin\alpha \sin\beta \sin\theta)$$ Then, the angle $\psi$ between the generator $OP$ and tangent vector $P'$ satisfies $$\cos\psi = \frac{P\cdot P'}{|P|\,|P'|}$$ We have $$\begin{align} P\phantom{^\prime}\cdot P' &= \frac{v \sin\beta \sin(\alpha+\beta) \sin\theta}{ \sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta} \\[4pt] |P\phantom{^\prime}|^2 = P\phantom{^\prime}\cdot P\phantom{^\prime} &= \frac{v^2 \sin^2(\alpha+\beta)}{(\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta)^2} \\[4pt] |P'|^2 = P'\cdot P' &= (\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta)^2 + \sin^2\beta \sin^2\theta \end{align}$$ Thus,

$$\begin{align} \cos\psi &= \phantom{\pm}\frac{\sin\beta \sin\theta}{\sqrt{(\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta)^2 + \sin^2\beta \sin^2\theta}} \\[4pt] \sin\psi &= \pm\frac{\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta}{\sqrt{(\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta)^2 + \sin^2\beta \sin^2\theta}} \\[4pt] \cot\psi &= \pm\frac{\sin\beta\sin\theta}{\sin\alpha\cos\beta - \cos\alpha\sin\beta\cos\theta} = \pm\frac{\sin\theta}{\sin\alpha\cot\beta - \cos\alpha\cos\theta} \\[4pt] \end{align} $$

for appropriate choices of sign. $\square$

(I was hoping for something a little more elegant.)

---

Incidentally, one can show that, in general, the eccentricity of the conic is given by $e = \sin\beta/\sin\alpha$, but this observation doesn't seem to make the formulas appreciably better.

---

For the "standard" cone with $\alpha=\pi/4$, we have $$\cot\psi = \pm\frac{\sqrt{2}\,\sin\theta}{\cot\beta-\cos\theta}$$

• For any cone cut by a horizontal plane, $\beta=0$ (giving a circle), we have $$\cot\psi = 0$$ so that $\psi$ is constantly $\pi/2$, which is geometrically obvious (as noted by OP).

• For the standard cone cut by a vertical plane, $\beta=\pi/2$ (giving a rectangular hyperbola), we have $$\cot\psi = \pm \sqrt{2}\tan\theta \quad\to\quad \cot\theta\cot\psi = \pm\sqrt{2}$$ The reader can verify that this agrees with @Aretino's formula, with the condition $a=b$.

• For the standard cone cut by a comparably-inclined plane, $\beta=\alpha=\pi/4$ (giving a parabola), we have $$\cot\psi = \pm\frac{\sqrt{2}\,\sin\theta}{1-\cos\theta} = \pm\sqrt{2}\,\cot\frac12\theta$$

Answer 2

WARNING: this solution refers only to the case when the plane is perpendicular to the base of the cone. See Blue's answer for the general case.

Let $G'$ be the projection of $G$ (vertex of the hyperbola) on the axis of the cone, $H$ the projection of $P$ on the axis of the hyperbola and $H'$ be the projection of $H$ on the axis of the cone. If we set: $$ x=OH',\quad y=PH,\quad a=OG',\quad b=GG'=HH', $$ it is easy to show that the usual equation holds: $$ \tag{1} {x^2\over a^2}-{y^2\over b^2}=1. $$ If $T$ is the intersection of the tangent at $P$ with the axis $GH$ of the hyperbola, and $T'$ is the projection of $t$ on the axis of the cone, then we find $$ OT'={a^2\over x}. $$ The lengths of $PT$, $PO$ and $OT$ can be now found as a function of $a$, $b$, $x$, $y$, and $\psi=\angle OPT$ can be computed by the cosine rule as: $$ \tag{2} \cos\psi={\displaystyle\left(1+{b^2\over a^2}\right)x^2-b^2-a^2\over \displaystyle x\sqrt{1+{b^2\over a^2}} \sqrt{\left(1+{b^2\over a^2}\right)x^2 +{a^4\over x^2}-2a^2-b^2} }. $$ If $\theta=\angle PH'H$ is the usual azimuthal angle, then $$ \tag{3} \tan\theta={y\over b} \quad\text{and}\quad x^2=\left(1+{y^2\over b^2}\right)a^2={a^2\over\cos^2\theta}. $$ Substituting that into $(2)$ finally gives: $$ \cos\psi={\sqrt{a^2+b^2}\sin\theta\over\sqrt{a^2\sin^2\theta+b^2}}. $$