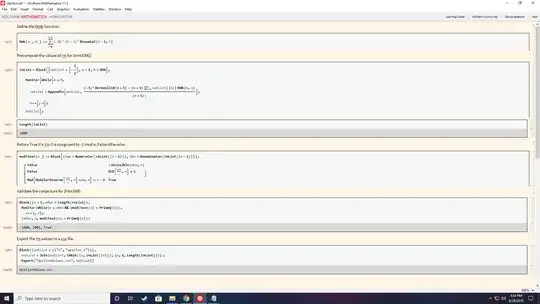
The Bernoulli numbers $B_n$. where all numbers $B_n$ are zero with odd index $n>1$. first values are given by $B_{0} = 1$ , $B_{1} = -1/2$, $B_{2} = 1/6$, $B_{3} = -1/30$.
Agoh conjecture: let $n$ be a positive integer with $n \ge 2$, then
$$nB_{n-1} \equiv -1 \pmod{n}\iff n\text{ is prime} $$
The idea of $\Upsilon$ number comes from my power sum formula and negative values of zeta function
Definition let $m$ be a non-negative integer $$\zeta(-m)=(-1)^{m}\frac{B_{m+1}}{m+1}=\sum_{b=1}^{m+1} \Upsilon_b\sum_{i=0}^{b-1} (-1)^{i}(b-i)^{m}\binom{b-1}i$$
so we can calculate values of $\Upsilon_b$ , if we substitute value $\zeta (0)=-1/2$ gives $\Upsilon_1=-1/2$.
Again we can calculate next value using or substituting previous values of $\Upsilon_b$.
first values are given by $$\begin{align*} \Upsilon_1&=-\frac{ 1}{2},\\ \Upsilon_2&=\frac{ 5}{12},\\ \Upsilon_3&=-\frac{ 3}{8},\\ \Upsilon_4&=\frac{ 251}{720},\\ \Upsilon_5&=-\frac{ 95}{288},\\ \Upsilon_6&=\frac{ 19087}{60480},\\ \Upsilon_7&=-\frac {5257}{17280}. \end{align*}$$
hypothesis: let $n$ be a positive integer with $n \ge 2$, then
<p><span class="math-container">$$n\Upsilon_{n-1} \equiv -1 \pmod{n} \iff n\text{ is prime} $$</span></p> <p>Else show that hypothesis is equivalence to agoh's conjectures</p> <p>Else show that if n is prime then <span class="math-container">$n\Upsilon_{n-1} \equiv -1 \pmod{n} $</span></p>Steven Clark had verified conjecture $n\Upsilon_{n-1} \equiv -1 \pmod{n}\iff n\in \mathbb{P}$ for $2 \leq n \leq 500 $
More simply
Let $D_{m,b}=\sum_{i=0}^{b-1} (-1)^{i}(b-i)^{m}\binom{b-1}i$
So $D_{m,m+1}=m!$
$$\Upsilon_{m+1}=\frac{(-1)^{m}B_{m+1}-(m+1)(\Upsilon_1 D_{m,1}+\Upsilon_2 D_{m,2}+\cdots+\Upsilon_m D_{m,m})}{(m+1)!}$$