3

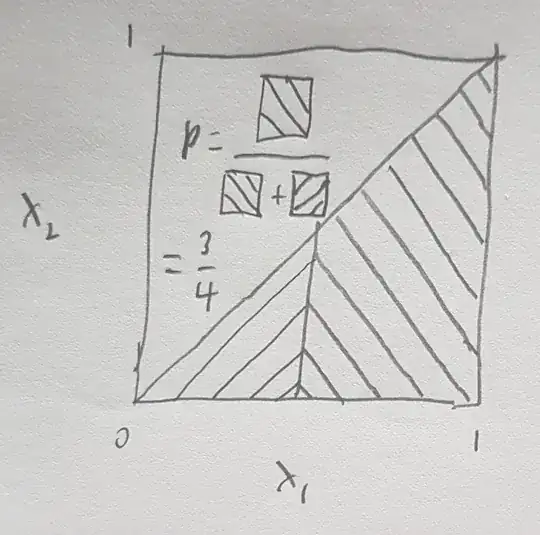
Assume $X_{1}$ and $X_{2}$ are independent random variables both drawn from a uniform distribution with support between 0 and 1, i.e $\mathbb{U}\left[0,1 \right]$.

I am interested in the following probability:

$$ Prob(X_{1}>0.5 | X_{1}>X_{2}) $$

Can someone help me showing me how to compute this probability? I really have no idea.

This is a related question in which I need to understand how to compute this type of objects: Using Law of Total Probability to compute cdf of the maximum of RVs

econ_ugrad
  • 101

2 Answers2

2

Geometrically speaking…

The answer is $\frac34$.

Parcly Taxel
  • 105,904
2

Adding the integral way $$p(x>.5 \cap x>y) = \int_.5^1 \int_0^x dy dx = \frac{1}{2}-\frac{1}{8} = \frac{3}{8}$$

then $p(x>y)$ is $\frac{1}{2}$ by symmetry or we can use the law of total probability.

$$p(x<.5 \cap x>y) = \int_0^.5 \int_0^x dy dx = \frac{1}{8} $$ $$p(x>y) \frac{3}{8}+\frac{1}{8} = \frac{1}{2}$$

so,

$$p(x>.5|x>y) = \frac{3}{8} \frac{2}{1} = \frac{3}{4}$$

Sam
  • 36