Minimize $\| A x - b \|_{2}^{2}$ Subject To $\| x \|_2 = 1$ and $x \succeq 0$ (Least Squares with Inequality and Non Linear Equality of $ L_2 $ Norm)

Question

Given $y \in \mathbb R^n$ and $A \in \mathbb R^{n \times n}$, whis is some way for

$$\min_x \| y- Ax\|$$ subject to $\|x\|=1$, and $x \geq 0$ (which means every components of $x$ is nonnegative)?

Is there any book discussing such a problem? Thanks!

Remark: The objective functions $\left\| A x - y \right\|$ and $\frac{1}{2} {\left\| A x - y \right\|}$ are equivalent, while the latter is differentiable and easier to handle.

Answer 1

You didn't specify but I presume you mean to use the Euclidian norm. Your problem is nonconvex so in general you won't be able to find an analytical expression for a solution.

The problem without the bound constraints $$ \min \|Ax-b\| \quad \text{subject to} \ \|x\| = \Delta $$ is well understood and, despite the fact that it is nonconvex, we have a characterization of its global solutions from the Gay-Dennis-Welsh theorem. See for instance Theorem 7.2.1 in http://www.ec-securehost.com/SIAM/MP01.html It may be found numerically using the method of Moré and Sorensen (described in the same book).

The problem without the norm constraint is also well understood and you'll find in fact methods for the problem where the norm constraint is a inequality instead of an equality, i.e., $$ \min \|Ax-b\| \quad \text{subject to} \ \|x\| \leq \Delta, \ x \geq 0 $$ in standard textbooks on linear least-squares problems because this problem is closely related to the regularized least-squares problem $$ \min \|Ax-b\| + \delta \|x\| \quad \text{subject to} \ x \geq 0. $$ These are convex problems. See for instance Chapter 5 in http://www.ec-securehost.com/SIAM/ot51.html or Chapters 20-23 in http://www.ec-securehost.com/SIAM/CL15.html

As someone else mentioned, interior-point methods are of interest for the convex problem ($\|x\| \leq \Delta$) but they can also be applied to the nonconvex problem ($\|x\| = \Delta$). However, you'll have to apply a generic interior-point method that won't be able to exploit your least-squares structure. I'm not aware of a method specifically designed for your problem.

I hope this already helps.

(I'm not affiliated with SIAM but they happen to have a great book collection.)

Answer 2

The problem does not have an analytical solution but can be easily solved using a projected gradient method. Let us rewrite your problem in an equivalent form:

\begin{align} \min_x~& \frac{1}{2}\Vert Ax-b\Vert^2\\ s.t.~& \Vert x\Vert =1\\ & x\geq 0\end{align}

The method works as follows:

• Let $x_0$ be a feasible point (eg $x_0=0$), and let $k=1$.
• At iteration $k$, perform a gradient step followed by a projection step. For the grdient step, let $\tilde{x}_k=x_{k-1}-\alpha_k g_{k-1}$, where $g_{k-1}=A^T(Ax_{k-1}-b)$ is the gradient of the objective function at $x_{k-1}$ and $\alpha_k$ is the step length, found for example via a line search. Then for the projection step, let $\tilde{x}_k=max(\tilde{x}_k,0)$ (component-wise) and then $x_k=\tilde{x}_{k}/\Vert \tilde{x}_{k}\Vert$. If the stopping criterion is met, stop, otherwise let $k=k+1$ and perform the step again.

As an illustration, I have let $A=\begin{pmatrix} 1&0\\0&3\end{pmatrix}$ and $b=\begin{pmatrix} 3\\2\end{pmatrix}$ and obtained the following iterates:

Answer 3

How about using Lagrange function? Let $\|\cdot\|$ be the euclidian norm, then You can define the Lagrangian as $$ L(x,\lambda,\mu)=\|y-Ax\|^{2}+\lambda\cdot(\|x\|^{2}-1)+\mu\cdot x, $$ where $\mu\in R^{n}$ is the Lagrange parameter for the inequality constraint and $\lambda\in R$ for the equality constraint. I squared the norms to get differentiability. This should be ok. Now You could compute derivatives etc...to get points which are candidates for optimal points (then use constraint qualifications...) Maybe this works and is helpful?

Answer 4

If $A$ is non-singular, then I think $x = A^{-1}y / ||A^{-1}y||$ is the solution (the image of the unit ball under $A$ will be convex, so the minimum is attained when $Ax \parallel y$).

If $A$ is singular, I think you can start like you would without the $||x|| = 1$ restriction - replace $y$ with the orthogonal projection of $y$ onto the column space of $A$ (call it $y'$), then solve $\min||y'-Ax||$ like in the first case (find $x'$ so $Ax' = y'$, then normalize $x'$ to find $x$).

Answer 5

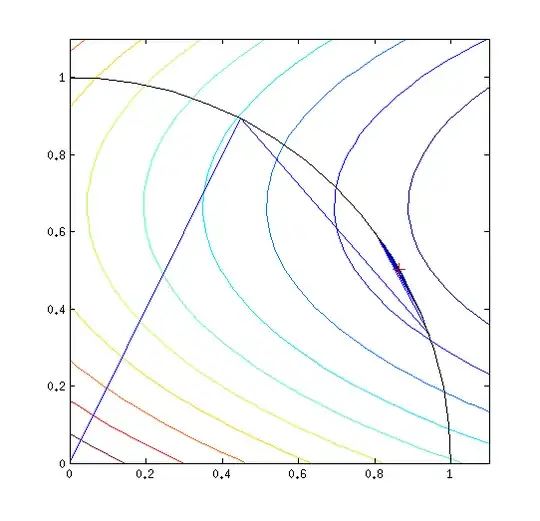
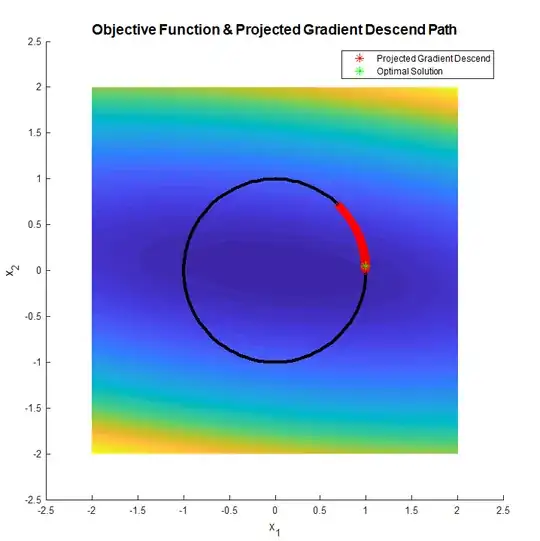
In simple form the system is $$min_{x_1,x_2,...,x_n}\sqrt{\sum_{i=1}^n (y_i-A_{i,1}x_1-A_{i,2}x_2-...-A_{i,n}x_n)^2}$$ $$s.t.\quad \sqrt{\sum_{i=1}^n x_i^2}-1=0$$ where the Lagrangian becomes $$L=\sqrt{\sum_{i=1}^n (y_i-A_{i,1}x_1-A_{i,2}x_2-...-A_{i,n}x_n)^2}+\lambda \bigg({\sqrt {\sum_{i=1}^n x_i^2}-1}\bigg )$$ By taking partial derivatives $$\frac{\partial L}{\partial x_1}=\frac{\lambda x_1}{\sqrt{\sum_{i=1}^n x_i^2}}-\frac{\sum_{i=1}^nA_{i,1}(y_i-A_{i,1}x_i)}{\sqrt{\sum_{i=1}^n (y_i-A_{i,1}x_1-A_{i,2}x_2-...-A_{i,n}x_n)^2}}=0$$ $$\frac{\partial L}{\partial x_2}=\frac{\lambda x_2}{\sqrt{\sum_{i=1}^n x_i^2}}-\frac{\sum_{i=1}^nA_{i,2}(y_i-A_{i,2}x_i)}{\sqrt{\sum_{i=1}^n (y_i-A_{i,1}x_1-A_{i,2}x_2-...-A_{i,n}x_n)^2}}=0$$ ... $$\frac{\partial L}{\partial x_n}=\frac{\lambda x_n}{\sqrt{\sum_{i=1}^n x_i^2}}-\frac{\sum_{i=1}^nA_{i,n}(y_i-A_{i,n}x_i)}{\sqrt{\sum_{i=1}^n (y_i-A_{i,1}x_1-A_{i,2}x_2-...-A_{i,n}x_n)^2}}=0$$ $$\frac{\partial L}{\partial \lambda}=\sqrt {\sum_{i=1}^n x_i^2}-1=0$$ Now you have n+1 nonlinear equation which you can solve for n+1 variables by using some numerical method.

PS: I skipped the positivity of x's. You can hardcode it by Kuhn-Tucker conditions which can make the system too complicated; or you can check your solution set afterwards.

Answer 6

I would use the Projected Gradient Descend for this case.
Though the problem isn't Convex it will work nicely.

The algorithm is as following:

1. Calculate the Gradient at the current point.
2. Update the solution $ x = x - t {A}^{T} A x - {A}^{T} b $ where $ {A}^{T} A x - {A}^{T} b $ is the Gradient of the Objective Function at $ x $ and $ t $ is the step size.
3. Project the output of previous step into $ {\mathbb{R}}_{+} $ by $ {x}_{i} = \max \left\{ {x}_{i}, 0 \right\} $.
4. Project the output of previous step onto the Unit Sphere by $ {x}_{i} = \frac{ {x}_{i} }{ \left\| x \right\|_{2} } $.
5. Go back to (1) (Or check validity of the point, KKT will do even the problem isn't Convex).

In a simple 2D example I created it worked pretty well:

The code is available at my StackExchange Mathematics Q2699867 GitHub Repository.

Remark 001
I'd even considering starting with the solution of the Convex Problem when you replace the equality constraint $ \left\| x \right\|_{2} = 1 $ by $ \left\| x \right\|_{1} = 1 $. You can either use it as a starting point for the above algorithm or approximated solution by itself.

Remark 002
Another approach might be something like I did in - Solution for $ \arg \min_{ {x}^{T} x = 1} { x}^{T} A x - {c}^{T} x $.
Yet after each iteration of updating $ \lambda $ you should also project the output $ x $ into $ \mathbb{R}_{+} $.