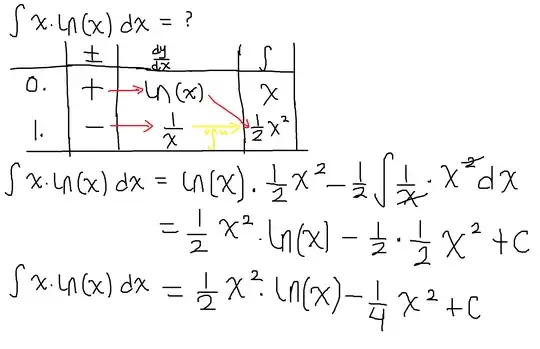Suppose $\frac{dy}{dx}=x\ln x,$ my teacher asks me to find $y$.
So I assume I got to integrate the right hand side:
$$\int x\ln x\, dx$$
The result I got is $$ \int x\ln x\, dx=x\ln x-x+C\tag{1} $$ But, apparently, it is wrong since taking the derivative gives: $$ (x\ln x-x+C)'=\ln x+1-1=\ln x. $$
Can you please give me a hand?
The answe you got is wrong indeed, since
$$(x\ln x - x)' = 1\cdot \ln x + x\cdot \frac{1}{x} - 1 = \ln x + 1 - 1 = \ln x\neq x\ln x$$
To calculate the integral, use the per partes method. Since $$\int u(x)v'(x)dx = u(x)v(x) - \int u'(x) v(x)dx,$$ you should select $u$ such that you can calculate its derivative, while $v'$ should be such that you can calculate its antiderivative. In your case, it should be clear which of the functions $x$ and $\ln x$ is easier to find the antiderivative of.
Hint use integration by parts and take proper 1st and 2nd function while solving the integration
$$\frac{dy}{dx}=x\ln x$$ $$\implies \int dy=\int x\ln x dx$$ $$\implies y=\ln x \int x dx-\int \left(\frac{d}{dx} \ln x\cdot\int x dx\right)dx$$ $$\implies y=\frac{1}{2}x^2~\ln x-\int\frac{1}{x}\cdot\frac{1}{2}x^2 dx$$ $$\implies y=\frac{1}{2}x^2~\ln x-\frac{1}{4}x^2+c$$
Integrating by parts:
$$\int a(x)b(x)dx = a(x)\int b(x) dx - \int \left(a'(x) \int b(x)dx\right)dx$$
Using Latex is tiring, so i will just use drawing.
Differentiating the answer will definitely get you into the function that you want to integrate earlier, im using Integration by parts with the table method
Hint: Use integration by parts and be careful, you integrated $\ln(x)$ but you have to integrate $\color{red}{x} \cdot \ln(x)$.
