3

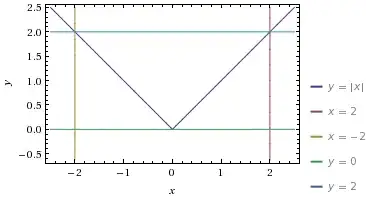
$${ x }^{ 2 }=4\\ \sqrt { { x }^{ 2 } } =\sqrt { 4 } \\ |x|=2$$ According to my professor, in the above case, the absolute value gives two solutions: $x=±2$ Consider the discriminant in the quadratic formula: $$x=\frac { -b±\sqrt { { b }^{ 2 }-4ac } }{ 2a } \\ Let\quad { z }^{ 2 }={ b }^{ 2 }-4ac\\ ±\sqrt { { b }^{ 2 }-4ac } \\ =±\sqrt { { z }^{ 2 } } \\ =±|z|\\ =±z$$ However, according to my professor, in this case, the absolute value gives only one solution: $|z|=z$

How come the absolute value sometimes gives one solution and sometimes it gives two solutions?

user1251385
  • 699

3 Answers3

3

Let's check this out, backwards, checking to see that the solutions $x = 2$ and $x = -2$ satisfy $|x| = 2$:

\begin{align} x &= 2: \quad &|2| &= 2 \\ \\ x &= -2: \quad &|-2| &= 2 \\ \\ \end{align}

There are TWO possible "input" values for $x$, such that $|x| = 2$. Note for each of the two inputs, the "output" is the same. Essentially the absolute value function can be described, defined as follows:

$\quad f:\mathbb R \to \mathbb R,\;f(x) = |x|:$

  • $\;x\mapsto -x\;\;$ if and only if $\;\;x \lt 0$,
  • $\;x \mapsto x,\;\;\;\;$ otherwise

I'll include a graph of the function $$f(x) = y = |x|,\;\;\text{with}\;\;x = -2,\;\; x = 2,\;\; f(x) = y = 2\;\;$$ to help you visualize the symmetric function, its behavior, and why $$\;f(x) = y = |x| = 2\;\implies\;x = -2\;\;\text{or}\;\;x = 2\;:$$

$\qquad\qquad\qquad\qquad$enter image description here


Graph from WolframAlpha

See also the following posts:

Community
  • 1
amWhy
  • 210,739
2

It's not that the absolute value doesn't give two solutions. It's just that if you have $±|z|$ this can either be $-(±z)$ or $(±z)$, either way you still only get two cases; namely, $±z$.

enter image description here

If you understand the equation $y=|x|$ then you should be able to see that since $|x|$ takes two values of $x$, both positive and negative, $|-x|=|x|$. So when you put in $x=-2$ you get 2, which is the same as if you plug in $x=2$. So it's symmetric.

MITjanitor
  • 2,728
  • 1
  • 23
  • 48
  • 1 more question: why do we bother with |x|? As shown in this diagram: http://s8.postimage.org/5n3zn5g6t/Untitled.png, the result will always be ±x, right? – user1251385 Mar 14 '13 at 02:15
  • But I mean: is there a reason to not shortcut it to just ±x? Is there any advantage to using |x| over ±x? – user1251385 Mar 14 '13 at 02:20
  • $|x|$ is an operation on $x$. We only say plus or minus $x$ if we're solving for $x$. We have to realize that $x$ could have been two values, $-x$ or $x$. – MITjanitor Mar 14 '13 at 02:22
1

Absolute value is a single value. But there are two cases, when $x\geq0$, $|x|=x$ and when $x<0$, $|x|=-x$. Since there is $\pm$ sign in your second last line, it does not really matter to separate the two cases. So simply $\pm |z|=\pm z$.

NECing
  • 4,251