Regularization of $\sum_{n=2}^\infty (-1)^n \log n$

Question

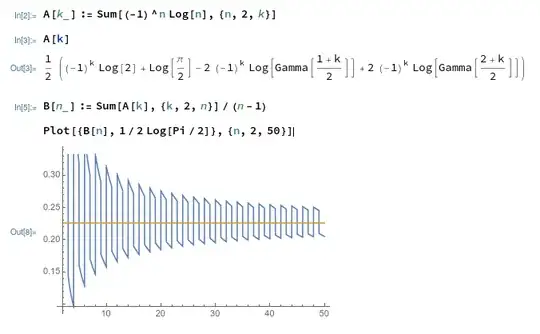
I accidentally stumbled on the following regularization of this divergent series:

$$\sum_{n=2}^\infty (-1)^n \log n "=" \frac{1}{2} \log \frac{\pi}{2}$$

I'm not familiar enough with regularization, so I wanted to ask if this result agrees with any other known regularization method?

I derived this result in the following way:

$$\log n=\int_0^\infty \frac{dx}{x} (e^{-x}-e^{-n x})$$

Now consider the function:

$$\sum_{n=2}^\infty (-1)^n (\log n) s^n=\int_0^\infty \frac{dx}{x} \left(e^{-x} \frac{s^2}{1+s}-\frac{s^2 e^{-2 x}}{1+s e^{-x}} \right)$$

$$\sum_{n=2}^\infty (-1)^n (\log n) s^n= \frac{s^2}{1+s}\int_0^\infty \frac{e^{-x}dx}{x} \frac{e^x-1}{e^x+s} $$

The right hand side converges for any $s>0$, and in particular, for $s=1$ we have:

$$\frac{1}{2}\int_0^\infty \frac{e^{-x}dx}{x} \frac{e^x-1}{e^x+1}=\frac{1}{2} \log \frac{\pi}{2}$$

I got the result with Wolfram Alpha, but I'm sure there's a proof somewhere on this site.

---

There's an interesting corollary here. If we write:

$$\sum_{n=2}^\infty (-1)^n (\log n) s^{n-1}= \frac{s}{1+s}\int_0^\infty \frac{e^{-x}dx}{x} \frac{e^x-1}{e^x+s} $$

And then integrate w.r.t. $s$ from $0$ to $1$, we obtain:

$$\sum_{n=2}^\infty (-1)^n \frac{\log n}{n}= \int_0^\infty \frac{\log(1+e^{-x})-e^{-x} \log 2}{x} dx= \gamma \log 2- \frac{\log^2 2}{2}$$

Answer 1

We can "calculate" the sum using the Wallis product formula.

Denoting our sum by

$$f = \sum_{n=1}^\infty (-1)^n \log(n)$$

we have

$$f= \log(2) - \log(3) + \log(4) \mp ...$$

and

$$e^f = \frac{2}{3} \frac{4}{5} \frac{6}{7} ...$$

Taking the square gives

$$e^{2f} = \frac{2}{3} \frac{2}{3} \frac{4}{5} \frac{4}{5} \frac{6}{7}...$$

Adding a factor $1$ in the denominator we arrive at

$$e^{2f} = \frac{2}{1} \frac{2}{3} \frac{4}{3} \frac{4}{5} \frac{6}{5} ...$$

But this is the famous Wallis product which has the value $\frac{\pi}{2}$.

Hence we have derived

$$f = \frac{1}{2} \log(\frac{\pi}{2})$$

The "regularization" is hidden somewhere in the sloppy derivation.

Answer 2

It is the usual $\zeta$-regularization, the same leading to $\sum_{n\geq 1}n "="-\frac{1}{12}$.
For any $s$ with positive real part we have $$ \eta(s)=\sum_{n\geq 1}\frac{(-1)^{n+1}}{n^s}=(1-2^{1-s})\zeta(s)$$ $$ -\eta'(s) = \sum_{n\geq 1}\frac{(-1)^n}{n^s}\log(n)=2^{-s} (\log(4)\zeta(s)-2\zeta'(s) + 2^s\zeta'(s))$$ and $\zeta(0)=-\frac{1}{2}$, $\zeta'(0)=-\log\sqrt{2\pi}$.

Answer 3

Using Cesàro summation seems to work. We take the partial average $$ A_k = \sum_{n=2}^k (-1)^n \log(n) = \cdots $$ then we take the mean of these $$ B_m = \frac{1}{m-1}\sum_{k=2}^m A_k $$ if we plot $B_m$ and your constant together there appears to be agreement in the large $m$ limit.

Here is an example in Mathematica: