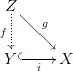1

I come across following theorem:

Universal property of subspace topology: $X$ is any topological space $Y\subset X$ $Z$ is any another topological space if there is continuous map $g:Z\to X$ such that $\operatorname{im}(g)\subset Y=\operatorname{im}(i)$ where $i:Y\to X$ inclusion map. then there exist continuous map such that $f:Z\to Y$ such that following diagram commutes and g realises $Z$ as subspace of $X$ iff f realises $Z$ as subspace of $Y$:

enter image description here

I do not understand why such theorem is required?

If some one gives me motivation about such theorem named as universal theorem It would be very useful.

Any help will be appreciated

Martin Sleziak
  • 56,060
Curious student
  • 6,915

1 Answers1

0

Such a theorem implies that if $f: X \to Y$ is continuous and $f[X] \subseteq Z \subseteq Y$ and $Z$ gets the subspace topology wrt $Y$, then $f: X \to Z$ (so changing only the codomain) is also continuous.

Henno Brandsma
  • 250,824