PDF of distance from origin to simplex in high dimension

Question

Let $\Delta^{n-1}$ be the standard simplex in $n$ dimensions:

$$ \Delta^{n-1} = \{ \mathbf{x}\in \mathbb{R}^n: \sum_i x_i=1 , \mathbf{x}\geq0\} $$

And assuming that we are uniformly sampling points $\mathbf{X}$ from this simplex, then the Euclidean distance $|\mathbf{X}|$ can also be considered a random variable. In the limit of $n\rightarrow\infty$, does the probability distribution of $|\mathbf{X}|$ approach some limit distribution that can be written in closed form?

Answer 1

Let's change a bit the symbols and define $$ \eqalign{ & T(n - 1,c) = \left\{ {{\bf x} \in R^{\,n} \;:\;\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} } = c\quad \left| {\;0 \le x_{\,k} } \right.} \right\} \cr & U(n,c) = \left\{ {{\bf x} \in R^{\,n} \;:\;\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} } \le c\quad \left| {\;0 \le x_{\,k} } \right.} \right\} \cr} $$

Let's then introduce a second euclidean reference system $\bf y$, having the $y_n$ axis aligned with the diagonal axis $x_1=x_2=\cdots = x_n$, normal to $T(n-1,c)$ $$ {\bf y} \in R^{\,n} \;:\;{\bf y} = {\bf Q}\,{\bf x}\; \wedge y_{\,n} = {1 \over {\sqrt n }}\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} } $$ The matrix $Q$ being orthogonal.

Indicating by $V(n,\, c)$ the volume of $U(n,\, c)$, and by $A(n-1,\, c)$ the volume of $T(n-1,\, c)$, we know that $V(n,\, c)=c^n/n!$ and that the relation with $A(n-1,\, c)$ is given by $$ \eqalign{ & V(n,c) = {{c^{\,n} } \over {n!}} = \cr & = \mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n,\,c)} dx_{\,1} \cdots dx_{\,n} = \mathop {\int { \cdots \int {} } }\limits_{{\bf y}\, \in \,U(n,\,c)} dy_{\,1} \cdots dy_{\,n} = \cr & = \int_{t = 0}^{\;c} {\left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,T(n - 1,\,t)} dy_{\,1} \cdots dy_{\,n - 1} } \right){{dt} \over {\sqrt n }}} = \cr & = {1 \over {\sqrt n }}\int_{t = 0}^{\;c} {A\left( {n - 1,t} \right)dt} \cr} $$ so that $$ \eqalign{ & A\left( {n - 1,c} \right) = \sqrt n {{c^{\,n - 1} } \over {\left( {n - 1} \right)!}}\quad \left| {\;A\left( {1,c} \right) = \sqrt 2 \,c} \right. \cr & V\left( {n,c} \right) = \int_{t = 0}^{\;c} {V\left( {n - 1,t} \right)dt} = {{c^{\,n} } \over {n!}} \cr & {{A\left( {n,c} \right)} \over {\sqrt {n + 1} }} = \int_{t = 0}^{\;c} {{{A\left( {n - 1,t} \right)} \over {\sqrt n }}dt} = {{c^{\,n} } \over {n!}} \cr} $$

Coming to the problem, we are practically asked to determine the 2nd moments of T(n-1,1) wrt the origin.
Let's start and determine the moments of U(n,c): $$ \eqalign{ & Y(n,c) = \mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n,\,c)} \left( {\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} ^2 } } \right)dx_{\,1} \cdots dx_{\,n} = \cr & = \mathop {\int { \cdots \int {} } }\limits_{{\bf y}\, \in \,U(n,\,c)} \left( {\sum\limits_{1\, \le k\, \le \,n} {y_{\,k} ^2 } } \right)dy_{\,1} \cdots dy_{\,n} = \cr & = \int_{t = 0\;}^{\;c} {\left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf y}\, \in \,T(n - 1,\,t)} \left( {\sum\limits_{1\, \le k\, \le \,n} {y_{\,k} ^2 } } \right) dy_{\,1} \cdots dy_{\,n - 1} } \right){{dt} \over {\sqrt n }}} = \cr & = \int_{t = 0}^{\;c} {\left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,T(n - 1,\,t)} \left( {\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} ^2 } } \right) dA\left( {n - 1,t} \right)} \right){{dt} \over {\sqrt n }}} \cr} $$

Then $$ \sqrt n {d \over {dc}}Y(n,c) = \mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,T(n - 1,\,c)} \left( {\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} ^2 } } \right) dA\left( {n - 1,c} \right) = I(n - 1,c) $$ and $$ {{I(n - 1,1)} \over {A(n - 1,1)}} $$ will give the required expected value of the sum.

Let's put up a recursion to compute $Y(n,c)$. $$ \eqalign{ & Y(n,c) = \mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n,\,c)} \left( {\sum\limits_{1\, \le k\, \le \,n} {x_{\,k} ^2 } } \right)dx_{\,1} \cdots dx_{\,n} = \cr & = \int_{x_{\,n} = 0}^{\;c} {\left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n - 1,\,c - x_{\,n} )} \left( {\left( {\sum\limits_{1\, \le k\, \le \,n - 1} {x_{\,k} ^2 } } \right) + x_{\,n} ^2 } \right)dx_{\,1} \cdots dx_{\,n - 1} } \right)dx_{\,n} } = \cr & = \int_{t = 0}^{\;c} {t^{\,2} \left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n - 1,\,c - t)} dx_{\,1} \cdots dx_{\,n - 1} } \right)dt} + \cr & + \int_{t = 0}^{\;c} {\left( {\mathop {\int { \cdots \int {} } }\limits_{{\bf x}\, \in \,U(n - 1,\,c - t)} \left( {\left( {\sum\limits_{1\, \le k\, \le \,n - 1} {x_{\,k} ^2 } } \right)} \right)dx_{\,1} \cdots dx_{\,n - 1} } \right)dt} = \cr & = \int_{t = 0}^{\;c} {t\,^2 \;V(n - 1,\,c - t)dt} + \int_{t = 0}^{\;c} {Y\left( {n - 1,\,c - t} \right)dt} = \cr & = {1 \over {\left( {n - 1} \right)!}}\int_{t = 0}^{\;c} {t^{\,2} \;\left( {c - t} \right)^{\,n - 1} dt} + \int_{t = 0}^{\;c} {Y\left( {n - 1,\,c - t} \right)dt} = \cr & = {{c^{\,n + 2} } \over {\left( {n - 1} \right)!}}\int_{s = 0}^{\;1} {s^{\,2} \;\left( {1 - s} \right)^{\,n - 1} ds} + \int_{s = 0}^{\;c} {Y\left( {n - 1,\,s} \right)ds} = \cr & = {{c^{\,n + 2} } \over {\left( {n - 1} \right)!}}{\rm B}(3,n) + \int_{s = 0}^{\;c} {Y\left( {n - 1,\,s} \right)ds} = \cr & = {{2c^{\,n + 2} } \over {\left( {n + 2} \right)!}} + \int_{s = 0}^{\;c} {Y\left( {n - 1,\,s} \right)ds} \cr} $$

The first two values for $Y$ are $$ \eqalign{ & Y(1,c) = \int\limits_{0\, \le \,x\, \le \,c} {x^2 dx} = {{c^{\,3} } \over 3} \cr & Y(2,c) = \int\!\!\!\int\limits_{0\, \le \,x + y\, \le \,c} {\left( {x^2 + y^2 } \right)dxdy} = \cr & = \int_{y = 0}^c {\left( {\int_{x = 0}^{c - y} {\left( {x^2 + y^2 } \right)dx} } \right)dy} = \cr & = \int_{y = 0}^c {\left( {\left( {{{\left( {c - y} \right)^3 } \over 3} + y^2 \left( {c - y} \right)} \right)} \right)dy} = \cr & = {{c^4 } \over {12}} + {{c^4 } \over 3} - {{c^4 } \over 4} = {{c^4 } \over 6} = \cr & = {{2c^{\,4} } \over {4!}} + \int_{s = 0}^{\;c} {{{s^{\,3} } \over 3}ds} \cr} $$

The recurrence can be solved to give $$ Y(n,c) = {{2n} \over {\left( {n + 2} \right)!}}c^{\,n + 2} $$

and finally $$ {{I(n - 1,c)} \over {A(n - 1,c)}} = {{\sqrt n {d \over {dc}}Y(n,c)} \over {\sqrt n {{c^{\,n - 1} } \over {\left( {n - 1} \right)!}}}} = {2 \over {\left( {n + 1} \right)}}c^{\,2} $$

i.e., in your notation $$ E\left[ {\left| {\,{\bf X}\,} \right|^{\,2} } \right] = {2 \over {n + 1}} $$

Now, the PDF of each point is given by $dA(n-1,1)/A(n-1,1)$.
$dA(n-1,1)$ can be conveniently expressed in terms of the $y$ coordinates, but the bounds of $T(n-1,1)$ in terms of $0 \le x_k$ are not simply convertible into $y$.

For the case of $ f( \bf X)= |\bf X |$, we have better and use cylindrical coordinates around the diagonal axis, according to the following sketch

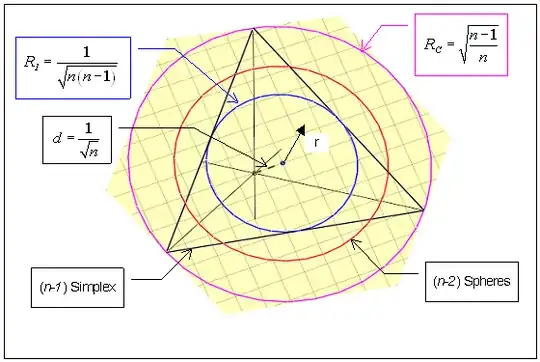
We can deduce that the PDF of $ x= |\, \bf X \, |$ will be
- null till $x$ reaches the distance of $T(n-1,1)$ from the origin: $d=1/ \sqrt{n}$;
- after that we will have that $x=\sqrt{d^2+r^2}$, where $r$ is the radius of a $(n-2)$-sphere, lying in the plane of $T(n-1,1)$ and centered with it;
- while $r$ increases from $0$ to the in-radius $R_I = 1/\sqrt{n(n-1)}$ the corresponding sphere remains inside the simplex, with a surface area of $$ S(n - 2) = {{2\pi ^{\,\,(n - 1)/2} } \over {\Gamma \left( {(n - 1)/2} \right)}}r^{\,n - 2} $$
- after $r$ has surpassed the in-radius, the sphere it individuates will partly debord out of the simplex, the circle in red in the sketch; the section of its area intercepted by the simplex will be that inside the solid angles defined by the vertices;
- the intercepted area will become null at the circum-radius $R_C = \sqrt{(n-1)/n}$.

The problem is that for high $n$, the volume gets concentrated on the border of the sphere. This makes so that the maximum of $PDF(r)$ moves beyond the in-radius and it becomes fundamental to express the area intercepted by the vertices.
I could not yet succeed in that, and could not find on the web a simple formulation .

--- 2nd step ---

Let's summarize our knowledge till here and introduce $J(n-1,c)$ as the sum of the 2nd moments of $T(n-1,c)$ wrt its centroid. $$ \left\{ \matrix{ d\left( {n,c} \right) = {c \over {\sqrt n }} \hfill \cr A\left( {n - 1,c} \right) = \sqrt n {{c^{\,n - 1} } \over {\left( {n - 1} \right)!}} \hfill \cr Y(n,c) = {{2n} \over {\left( {n + 2} \right)!}}c^{\,n + 2} \hfill \cr I(n - 1,c) = \sqrt n {d \over {dc}}Y(n,c) = {{2n\sqrt n } \over {\left( {n + 1} \right)!}}c^{\,n + 1} = \hfill \cr = A\left( {n - 1,c} \right)d\left( {n,c} \right)^{\,2} + J(n - 1,c) \hfill \cr J(n - 1,c) = I(n - 1,c) - A\left( {n - 1,c} \right)d\left( {n,c} \right)^{\,2} = \hfill \cr = {{\left( {n - 1} \right)\sqrt n } \over {\left( {n + 1} \right)!}}c^{\,n + 1} \hfill \cr S(n - 2,r) = {{2\pi ^{\,\,(n - 1)/2} } \over {\Gamma \left( {(n - 1)/2} \right)}}r^{\,n - 2} \hfill \cr R_{\,I} (n - 1,c) = {c \over {\sqrt {n\left( {n - 1} \right)} }} \hfill \cr R_{\,C} (n - 1,c) = {c \over {\sqrt {n/\left( {n - 1} \right)} }} \hfill \cr} \right. $$

Clearly we can write, in "polar coordinates", that $$ \left\{ \matrix{ J(n - 1,c) = {{\left( {n - 1} \right)\sqrt n } \over {\left( {n + 1} \right)!}}c^{\,n + 1} = \hfill \cr = \int_{r\, = \;0\;}^{\;R_{\,I} } {r^{\,2} \;S(n - 2,r)dr} + \int_{r\, = \;R_{\,I} \;}^{\;R_{\,C} } {r^{\,2} \;S_{\,P} (n - 2,r)dr} \hfill \cr A\left( {n - 1,c} \right) = \sqrt n {{c^{\,n - 1} } \over {\left( {n - 1} \right)!}} = \hfill \cr = \int_{r\, = \;0\;}^{\;R_{\,I} } {S(n - 2,r)dr} + \int_{r\, = \;R_{\,I} \;}^{\;R_{\,C} } {S_{\,P} (n - 2,r)dr} \hfill \cr} \right. $$ where $S_{\,P} (n - 2,r)$ is the surface of the sphere included in the simplex.

Using the duplication formula for Gamma $$ \Gamma \left( n \right) = {{2^{\,n - 1} } \over {\sqrt \pi }}\Gamma \left( {n/2} \right)\Gamma \left( {n/2 + 1/2} \right) $$

we reach then to $$ \eqalign{ & \int_{r\, = \;\;R_{\,I} (n - 1,\,c)\;}^{\;R_{\,C} (n - 1,\,c)} {S_{\,P} (n - 2,r)dr} = \cr & = \left( {{{n^{\,1/2} } \over {\Gamma \left( n \right)}} - {{2\pi ^{\,\,(n - 1)/2} } \over {n^{\,\,(n - 1)/2} \left( {n - 1} \right)^{\,\,(n + 1)/2} \Gamma \left( {(n - 1)/2} \right)}}} \right)c^{\,n - 1} = \cr & = \left( {1 - {{2^{\,n - 1} \;\pi ^{\,\,n/2 - 1} \;\Gamma \left( {n/2} \right)} \over {n^{\,\,n/2} \left( {n - 1} \right)^{\,\,(n - 1)/2} }}} \right)A\left( {n - 1,c} \right) = \cr & = \eta (n - 1)\;A\left( {n - 1,c} \right) \cr} $$

So, using in case also the formula for $J$, the problem comes to determine $\eta (n-1,r)$ knowing its integral from $R_I$ to $R_C$.

Answer 2

A simple way to get the expected value $\mathbb{E}[\lVert X\rVert^2]$, without relying on the Dirichlet distribution (what we are considering here being a spacial case of it, the symmetric Dirichlet distribution with $\alpha=1$). This is only computing this expectation, not addressing the full question).

It is well-known that sampling $X$ uniformly from the probability simplex is equivalent to sampling $n-1$ i.i.d. uniform r.v.'s $U_1,\dots, U_{n-1}$, sorting them (adding $U_0=0$ and $U_n=1$), and looking at the differences. From this, we get that $X_1$ is distributed as $\min(U_1,U_2,\dots,U_{n-1})$ , from which its pdf is easily seen to be $$ f(x) = (n-1)(1-x)^{n-2}, \qquad x\in[0,1] $$

But we have, by symmetry and linearity, $$ \mathbb{E}[\lVert X\rVert^2] = \sum_{i=1}^n \mathbb{E}[X_i^2] = n \mathbb{E}[X_1^2] $$ from which $$ \mathbb{E}[\lVert X\rVert^2] = n \int_0^1 (n-1)x^2(1-x)^{n-2} dx = \boxed{\frac{2}{n+1}} $$