5

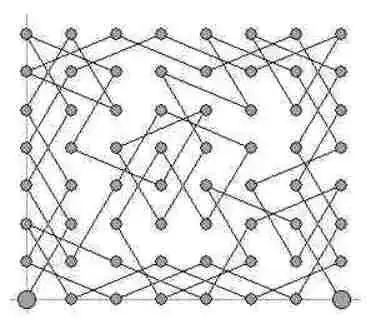
Is it possible to start with a knight at some corner of a chessboard and reach the opposite corner passing once through all the squares?

The knight can reach the other corner or any square for that matter. But if it were to pass through all the squares just for once, that means there should be 63 moves; the 63rd move being the one that it would make to reach the other corner. If the knight starts on a black square(1A), the other corner would also be black(8H). A knight reaches a square of the initial color after every even number of moves. 63 is an odd number, hence we've reached a contradiction. So, it is not possible.

Is my reasoning correct?

Also, is it possible for the knight to reach the vertically opposite end (say, 1A to 8A) passing through every square once?

Edit: I would appreciate a mathematical approach to prove that this is possible.

Edit 2: As pointed out in the answer, it is indeed possible to reach the vertically opposite end passing through every square once. I've been thinking along the same lines and I came up with this:

Since the 63rd move should land the knight (say, starting from white-1A) on the desired corner which is of the opposite color (black-8A in this case) and an odd number of moves results in a square of the alternate color, so this is possible.

Does this suffice to prove it?

Community
  • 1
Tapi
  • 1,763

1 Answers1

4

Yes, your reasoning is correct. As for a knight's tour from one corner to the other corner on the same edge, here's a very blurry image I found on the Internet. (The two large circles indicate start and finish.)

grid

Infiaria
  • 763
  • 1
    Interesting but I would appreciate a mathematical approach to prove that this is possible. – Tapi Jun 30 '19 at 13:27
  • 1
    @Tapi This tour, in particular, was generated using Warnsdorff's Rule, which is a heuristic method saying you should always move your knight to a square which has the least onward moves. – Infiaria Jun 30 '19 at 14:23