-1

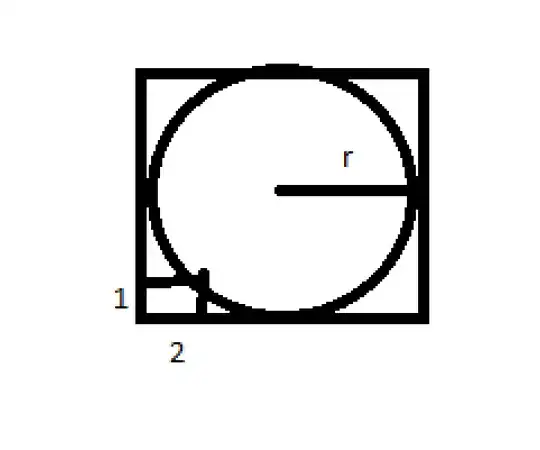
Find the radius of the circle inscbribed inside the square. The distance from the side of the square to circle is (2,1)see the attached image enter image description here

DonAntonio
  • 214,715
usmanharoon
  • 43
  • An ordered pair $;(2,1);$ is not "distance". It only seems to be the left lower vertex of he square is at the origin $;(0,0);$ and then $;(2,1);$ is a point on the circle... – DonAntonio Jun 26 '19 at 18:21
  • 2
    https://math.stackexchange.com/questions/2915935/radius-of-a-circle-touching-a-rectangle-both-of-which-are-inside-a-square/2915987#2915987 – Seyed Jun 26 '19 at 18:24

3 Answers3

1

Assuming the center at the origin we have $$x^2+ y^2=r^2$$ with the point $(-r+2, -r+1)$ on the circle.

Plugging in and simplifying the equation we get $$r^2-6r+5=0$$

The solution $r=5$ is acceptable.

Mohammad Riazi-Kermani
  • 69,891
0

Asuming the square's sides are parallel to the $\;x\,-$ axis and the $\;y\,-$ axis, and since the left lower vertex is at $\;(0,0)\;$ and the circle's equation is

$$(x-r)^2+(y-r)^2=r^2\;\;\;\text{(why?)}$$

we then get from the fact that $\;(2,1)\;$ is on the circle that

$$(2-r)^2+(1-r)^2=r^2\implies r=\ldots$$

Finish the argument

DonAntonio
  • 214,715
0

Using the Pythagoras theorem:
$a=1$ $cm$
$b=2$ $cm$
$(r-a)^2+(r-b)^2=r^2$
$(r-1)^2+(r-2)^2=r^2$
$r^2+1-2r+r^2+4-4r=r^2$
$r^2-6r+5=0$
$r=5$ $cm$
$r=1$ $cm$
The $r=5$ $cm$ is the acceptable answer.

Aditya Jain
  • 301