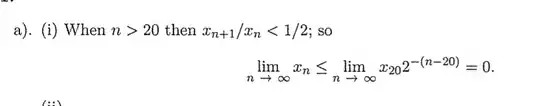My textbook is asking me to find the limit of $\frac{10^n}{n!}$. Here is how they do it:
My question is: Is this the only way to prove that the limit is $0$ ?
I know the fact that factorials diverge 'faster' than exponential, so can I just state this? I mean how am I supposed to know that at $n>20$ the ratio is $<\frac{1}{2}$ ?
Or should I just say that for some $N$, there is $n>N$ s.t. the ratio of the successive terms become less than $1$ and hence the limit is $0$?
We have $$\frac{x_{n+1}}{x_n} = \frac{10^{n+1}/(n+1)!}{10^n/n!} = \frac{10}{n+1}$$ From here it's quite easy to tell that for $n\geq 20$, this ratio is less than $\frac12$.
You are, in some sense, not supposed to know this. You are supposed to know a bunch of different general tips and tricks for evaluating limits (along with the general grasp of algebra needed to actually use them), among them trying to evaluate $\frac{x_{n+1}}{x_n}$ when you suspect that the limit is $0$ or $\infty$. It may not be the first thing you try, but is should probably at latest be second or third.
When you have that the ratio at $n>20$ is less than $\frac{1}{2}$, you obtain that $\frac{10^n}{n!} < c \frac{1}{2^n}$ for some $c$. This now converges to $0$.
Consider positive series $\sum\frac{10^n}{n!}$. Let $a_n=\frac{10^n}{n!}$, and $$\lim_{n\to \infty}\frac{a_{n+1}}{a_n}=\lim_{n\to \infty}\frac{10}{n+1}=0.$$ So the positive series $\sum\frac{10^n}{n!}$ is convergent, and $$\lim_{n\to \infty}\frac{10^n}{n!}=0.$$
Option:
$e^x=1+x +x^2/2! +...x^k/k!+...$, converges for $x \in.\mathbb{R}.$
Hence $\lim_{n \rightarrow \infty} x^n/n!=0.$
Set $x=10$, i.e consider $e^{10}$.
You need to be specific about what it means that factorial grows faster than exponential. And if you think about it, it means that $$ \lim_{n\rightarrow\infty} \frac{a^n}{n!} = 0$$ This is basically what you need to prove, so you cannot use that in the proof. Comparing this sequence with a geometric series is the easiest way I know.
As for you last question, you need a bit stronger condition. If you have $x_n>0$ and can prove that there exist $q<1$ and $N$ such that for $n>N$ you have $$ \frac{x_{n+1}}{x_n} < q$$ then it is enough to prove that $x_n\rightarrow 0$. This is because you have then $$\forall n>N: x_{n} < x_{N} \cdot q^{n-N} \rightarrow 0$$ which means $$ \lim_{n \rightarrow \infty} x_n =0$$
Knowing just that $$ \frac{x_{n+1}}{x_n} < 1$$ is not enough, for example for $x_n = \frac{n}{2n-1}$ you have $$ \frac{x_{n+1}}{x_n} = \frac{(n+1)(2n-1)}{(2n+1)n} = \frac{2n^2+n-1}{2n^2+n} < 1$$ but $$ \lim_{n \rightarrow \infty} x_n = \frac12$$
Here is another approach which you may find useful.
After a certain value of $n$ the ratio of successive terms is less than $1$ and hence the sequence is decreasing after a certain point. Also every term of the sequence is positive and hence the sequence tends to a limit (remember, monotone and bounded sequences are convergent), say $L$, and we have $L\geq 0$. Since $$x_{n+1}=\frac{10}{n+1}\cdot x_n$$ it follows by taking limits that $L=0\cdot L$ so that $L=0$.
