Using the maximum modulus theorem in complex analysis, what is a good technique for finding the maximum of $|f(z)|$ on $|z|\le 1$, when $f(z)=z^2-3z+2$?
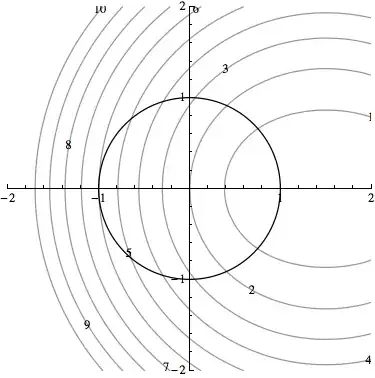
Got some really nice answers below, so I thought I'd share an image showing some contours of $|z^2-3z+2|$. Note that the magnitude does increase as we move "as far as possible" from the zeros (phrase used in answer below). And, at $z=-1$, note how the contour $|z^2-3z+2|=6$ is tangent to the circle $|z|=1$.