I am asked to calculate $(F^*w)(p)(v_1,v_2)$ given that $w=xydx+zdy+xdz$, $p=(1,-1,0)$, $v_1=(0,1,1),v_2=(1,0,1)$ and $F(x,y,z)=(e^y,e^x,e^y)$
As far as I am concerned, this should be an easy enough mechanical problem, however I just started studying differential forms and I am not sure I understand...
I know that $(F^*w)(p)(v_1,v_2)$ is defined as: $$(F^*w)(p)(v_1,v_2)=w(F(x))(dF_pv_1,dF_pv_2)$$ Therefore $w(F(x))=e^ye^xdx+e^ydy+e^ydz$ and $dF_p=\begin{bmatrix}0&e^{-1}&0\\e&0&0\\0&e^{-1}&0\end{bmatrix}$. Therefore $dF_pv_1=(e^{-1},0,e^{-1})^t,dF_pv_2=(0,e,0)^t$.
Now how do I follow?
Edit: Screenshot of the problem: 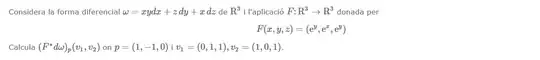 Translation: Consider the differential form ... of $R^3$ and the application ... given by
Translation: Consider the differential form ... of $R^3$ and the application ... given by
Calculate ... where