For our purposes we need to find at the least one case when a 50th percentile and the median aren't the same thing. I will present three such cases.
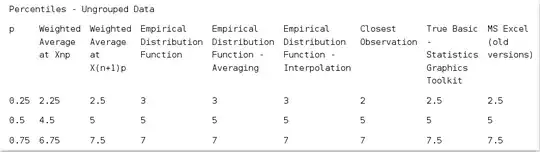
Here the first case (proof) goes as this: Suppose we have set of numbers {1,2,3}. Its median is 2. But 2 is NOT a 50th percentile because 2 isn't a percentile at all, it's a tertile. It has 1/3 of datapoints below it and 2/3 of datapoints below or equal to it.
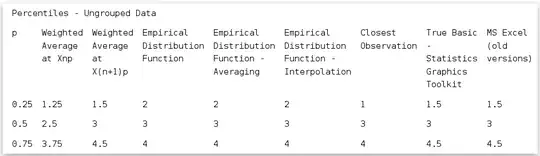
The second proof: Suppose we have set of numbers {1,2,3,4,5}. Its median is 3. But 3 is NOT a 50th percentile. For the inclusive definition of a percentile it's a 60th percentile, while for the exclusive definition it's a 40th percentile.
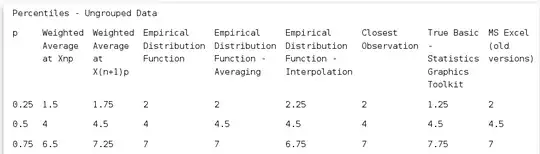
The third proof: Suppose we have a set of numbers {0,10}. Its median is 5. And it's also a 50th percentile. But there are other 50th percentiles that aren't equal to 5 (and thus, aren't medians), namely any number in interval [0;10) for the inclusive defintion of a percentile and any number in interval (0;10] for exclusive definition of a percentile.