What is a simple, physical situation where complex numbers emerge naturally?

Question

I'm trying to teach middle schoolers about the emergence of complex numbers and I want to motivate this organically. By this, I mean some sort of real world problem that people were trying to solve that led them to realize that we needed to extend the real numbers to the complex.

For instance, the Greeks were forced to recognize irrational numbers not for pure mathematical reasons, but because the length of the diagonal of a square with unit length really is irrational, and this is the kind of geometrical situation they were already dealing with. What similar situation would lead to complex numbers in terms that kids could appreciate?

I could just say, try to solve the equation $x^2 + 1 = 0$, but that's not something from the physical world. I could also give an abstract sort of answer, like that $\sqrt{-1}$ is just an object that we define to have certain properties that turn out to be consistent and important, but I think that won't be entirely satisfying to kids either.

Answer 1

I don't know

a simple, physical situation where complex numbers emerge naturally

but I can suggest a way to help you

teach middle schoolers about the emergence of complex numbers and I want to motivate this organically.

I did this once as a guest lecturer in a middle school classroom by developing a geometric interpretation of arithmetic on the number line.

Adding a fixed number $r$ is a shift by $r$, to the right if $r > 0$, to the left if $r < 0$. Successive shifts add the shift amounts. Each geometric shift is characterized by the position that $0$ moves to. You illustrate this visually by physically shifting a yardstick along a number line drawn on the board.

The answer to the question "what do you shift by so that doing it twice shifts by $r$?" is clearly $r/2$.

This is looking ahead to square roots, but you don't say that yet. The underlying idea is that the group of shifts is the additive group of the real numbers, but you don't say that ever.

Now that addition is done you go on to multiplication. Multiplying by a fixed positive $r$ rescales the number line. If $r>1$ things stretch, if $r < 1$ they shrink and multiplying by $r=1$ changes nothing. To know what a scaling does all you need to know is the image of $1$.

Successive scalings multiply, just as successive shifts add. What should you do twice to scale by $9$? Half of $9$ doesn't work, but $3$ does. The class will quickly grasp that the geometric way to halve a scaling is to find the square root.

What about multiplication by a negative number? The geometry is clear: it's reflection over $0$ followed by a scaling by the absolute value. Again the transformation is characterized by the image of $1$.

Now you're ready for the denoument. What geometric transformation can you do twice to move $1$ to $-1$ on the number line? Take your yardstick, place it on the line on the board, rotate by a quarter of a circle so that it's vertical, then another quarter and you're there. The image of $1$ is not on the line. It's at position $(0,1)$ in the cartesian coordinate system middle schoolers know about. They will find it cool to think of that point as a new number such that multiplying by it twice turns $r$ into $-r$. Name that number "$i$".

If you have brought the class along this far the rest is easy. They will quickly see the $y$ axis as the real multiples of $i$. Clearly adding $i$ should be a vertical translation by one unit. Vector addition for complex numbers follows quickly. Ask for the square root of $i$ and they will rotate the yardstick $45$ degrees. If they know about isosceles right triangles they will know that the (actually a) square root of $i$ is $(\sqrt{2}/2)(1+i)$, which they can check formally with the distributive law (which they will not ask you to prove).

---

A caveat. I think this should be pure fun for the class. Make that clear, so if some don't follow they don't worry. I would not try to integrate it into whatever the standard curriculum calls for. It should probably not extend over multiple class periods. Save it for a day near the end of the school year.

Answer 2

The historical origin of the complex numbers is, I think, the finest approach. Consider the problem of solving cubic equations of the type $x^3+px+q=0$. For this, you have Cardano's formula:$$x=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac q2-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}.$$But what do you do if it turns out that $\frac{q^2}{4}+\frac{p^3}{27}<0$? This happens, for instance, in the case of the equation $x^3-15x-4=0$; in this case we have $\frac{q^2}{4}+\frac{p^3}{27}=-121<0$. So, Cardano's formula tells us that a root of the equation is$$\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}.\tag1$$Could this mean that the equation has no solutions? No, since $4$ is clearly a solution. However, if we accept that we can work with square roots of negative numbers, then\begin{multline}\left(2+\sqrt{-1}\right)^3=2+11\sqrt{-1}=2+\sqrt{-121}\text{ and }\\\left(2-\sqrt{-1}\right)^3=2-11\sqrt{-1}=2-\sqrt{-121}.\end{multline}Therefore, it is natural to say that$$(1)=2+\sqrt{-1}+2-\sqrt{-1}=4.$$So, this shows that we can work with complex numbers in order to find real roots of cubic equations with real coefficients. And, in the XIX^th century, Pierre Wantzel proved that, if we wish to have an algebraic formula to do that, it is impossible to avoid complex numbers.

Answer 3

If you want a physical phenomenon for which complex numbers greatly simplify analysis, may I draw your attention to alternating electrical current?

You can either use calculus to analyze how a AC signal responds to a given circuit of resistors, capacitors, and inductors, or you can use complex numbers that turn all of this calculus into algebra.

Answer 4

I would suggest the Riemann sphere. It maps latitude and longitude onto a single number in a simple and delightful way. After you have done that, you can rotate the Earth about the North Pole by multiplying by $e^{i\theta}$, rotate it $90°$ about the equatorial points $90°W$ and $90°E$ by transforming $z$ to $\frac{1+z}{1-z}$, and even reflect it in the Greenwich meridian by transforming $z$ to $\bar z$. (The antipodal point of $z$ is $-\bar z^{-1}$ - nicely bringing in the idea that conjugation is a kind of reflection).

You can rotate a point $w$ onto the Pole (I usually use $0$ for the North Pole, though the convention seems to be to have that for the South Pole) by the transform that takes $z$ to $\frac{z-w}{1+wz}$. That lets you measure the great circle distance from any point $w_0$ to any other point $w_1$, since when you have moved $w_0$ to the Pole, the latitude of $w_1$ transformed the same way will easily give you its distance. You can get the direction too, by comparing the longitude of the transformed $w_1$ with the longitude of the transformed Pole.

And if you want to draw a great circle from $w_0$ to $w_1$, then all you need to do is take equal steps in latitude from the Pole to the transformed $w_1$, and do the inverse transform to take everything back to real latitudes and longitudes. I planned my first intercontinental flight that way.

All this is physical, as you requested. By encoding a pair of numbers (latitude and longitude) as a single complex number, it lets your pupils do all sorts of geographical and spherical-geometrical exercises just by multiplying and dividing complex numbers, without ever needing any formula full of sines and cosines.

As a bonus, if they are moving so fast through the cosmos that Special Relativity starts to have an effect, I learned from an article by Roger Penrose that one can still model the distorted positions of the stars by a transform of the form $\frac{a+bz}{c+dx}$. But that is left as an exercise for the reader.

Answer 5

Well..it may not be much use for middle-school students, but

http://www.feynmanlectures.caltech.edu/I_22.html

is pretty compelling.

One natural answer for middle-school students is that sine-waves look an awful lot like cosine-waves, and we have a ton of formulas tying them together in various ways, but if we introduce phase, then things get pretty. So we can describe a periodic value in terms of phase and amplitude. When we multiply these, the amplitudes and phases combine in a weird way, "weird" in the same way that instead of $$ \frac{a}{b} + \frac{c}{d} = \frac{a+c}{b+d} $$ we have to use more complicated rules to find the new numerator and denominator. But if we convert amplitude and phase to $x$-part and $y$-part via $$ x = A \cos \theta\\ y = A \sin \theta $$ then a product of waves ends up producing $x$ and $y$ values (i.e., real and imaginary parts) that combine with a rule no weirder than the one for adding fractions. The only peculiar thing is that $(0, 1) * (0, 1) = (-1, 0)$, so if you regard the "$x$-part" as corresponding to the real numbers, then you've got something whose square is $-1$.

Answer 6

While it's not "physical", I'd suggest perhaps the one "grade school" level introduction that is not artificial would, perhaps, ironically, be the one that is also that which motivated their creation in the first place and thus fits your bill of "something people were trying to solve that required their creation": the solution of a cubic polynomial.

I presume that, at this point, they have already heard of the quadratic formula. Then show them this:

$$x^3 + (3p)x - (2q) = 0$$

and ask how they'd go about solving that for $x$. Tell them it's clearly not a quadratic, as it involves a third power. How would you go about solving an equation with a third power? After a bit of wrestling with it, write that you can solve it with this:

$$x = \sqrt[3]{q + \sqrt{q^2 + p^3}} + \sqrt[3]{q - \sqrt{q^2 + p^3}}$$

which doesn't look too much worse than a quadratic formula. Play with a couple "easy" cases to show it works, then have them consider a case like $q = 2$, $p = -2$, i.e.

$$x^3 - 6x - 4 = 0$$

Show on a graph that it has 3 real solutions. Explain that this is the maximum possible number, because if you have all 3 solutions, you can factorize the polynomial and thus recover it completely therefrom, hence there can't be any missing. As a result, the formula for $x$ just given must give one of these 3 when you evaluate it.

But now ask them to try evaluating that formula, and see what happens under the square-root radicals. In particular, paying close attention to $q^2 + p^3$ with $q = 2$ and $p = -2$. Remember: $x$ is real, but something funny goes when you try to compute it this way.

Gerolamo Cardano was the first to discover the solution formula for the cubic polynomials in the 16th century, Renaissance Italy. When encountering a case like this, he also became the first to suggest the use of complex numbers, but called them merely a "subtle and useless" device. Nonetheless, they persisted and somewhat later another Renaissance Italian mathematician, Rafael Bombelli, would write down the codified rules for their arithmetical manipulation, and from then on their development would only continue further.

Answer 7

I recommend the geometric algebra approach to complex numbers.

We start with vectors in 2D. Vector addition and scalar multiplication are obvious (or just well-known). Vector multiplication is where it gets interesting. We assume that the product of vectors is associative, $\vec a(\vec b\vec c)=(\vec a\vec b)\vec c$, and that it distributes over addition. We also assume that a vector squared is its magnitude squared; if

$$\vec r=x\vec e_1+y\vec e_2$$

where $\vec e_1$ and $\vec e_2$ are the unit vectors along the $x$ and $y$ axes, then the Pythagorean theorem says

$$x^2+y^2=\vec r^2=x^2\vec e_1\!^2+xy\vec e_1\vec e_2+yx\vec e_2\vec e_1+y^2\vec e_2\!^2.$$

This requires that $\vec e_1\!^2=\vec e_2\!^2=1$, which makes sense because they're unit vectors. But it also requires that their product is anticommutative, $\vec e_1\vec e_2=-\vec e_2\vec e_1$. What is this quantity? Let's square it and see what happens:

$$(\vec e_1\vec e_2)^2=(\vec e_1\vec e_2)(\vec e_1\vec e_2)=\vec e_1(\vec e_2\vec e_1)\vec e_2=\vec e_1(-\vec e_1\vec e_2)\vec e_2=-(\vec e_1\vec e_1)(\vec e_2\vec e_2)=-1.$$

Any real number or vector would square to a positive number, so this is neither. This bivector $\mathbb i=\vec e_1\vec e_2$ can be thought of as the unit square for the plane (with a right-handed orientation; $-\mathbb i$ would be left-handed).

Multiplying a vector by $\mathbb i$ rotates it by $90^\circ$, clockwise if on the left, anticlockwise if on the right:

$$\vec e_1\,\mathbb i=\vec e_1\vec e_1\vec e_2=\vec e_2,\qquad\vec e_2\,\mathbb i=-\vec e_2\vec e_2\vec e_1=-\vec e_1$$

$$\vec r\,\mathbb i=-\mathbb i\,\vec r=x\vec e_1\,\mathbb i+y\vec e_2\,\mathbb i=-y\vec e_1+x\vec e_2.$$

Multiplying by $\mathbb i$ twice is thus a $180^\circ$ rotation, which flips the direction of the vector; $\vec r\,\mathbb i\,\mathbb i=-\vec r$. This provides one explanation of $\mathbb i^2=-1$.

More generally, multiplying a vector by a complex number $a+b\mathbb i$ rotates it by an arbitrary angle.

It's easy to convert a vector to a complex number or vice versa; just multiply by $\vec e_1$.

$$\vec e_1(x\vec e_1+y\vec e_2)=x+y\mathbb i$$

$$\vec e_1(a+b\mathbb i)=a\vec e_1+b\vec e_2$$

(There's nothing special about $\vec e_1$; any unit vector could be chosen for the "real axis".)

---

Links:

https://en.wikipedia.org/wiki/Geometric_algebra

http://www.mrao.cam.ac.uk/~clifford/publications/ps/imag_numbs.pdf

http://geocalc.clas.asu.edu/pdf/OerstedMedalLecture.pdf

Answer 8

I know you marked the question as answered but Impedance is a perfect physical phenomenon to show how complex numbers arise naturally. Impedance is kind of like regular resistance, but for AC circuits. Impedance behaves like a complex number, thus making it difficult to calculate the resistance (impedance) of AC circuits without using complex numbers.

Here is a snippet from Wikipedia regarding the phenomena:

In addition to resistance as seen in DC circuits, impedance in AC circuits includes the effects of the induction of voltages in conductors by the magnetic fields (inductance), and the electrostatic storage of charge induced by voltages between conductors (capacitance). The impedance caused by these two effects is collectively referred to as reactance and forms the imaginary part of complex impedance whereas resistance forms the real part.

In essence: If you try to calculate the impedance of AC circuits without complex numbers, you will only take the resistance part into consideration, not the reactance, thus giving you incorrect results.

Wikipedia article on electrical impedance

Answer 9

Here is an "un"-natural but possibly fun thought-experiment for middle schoolers, provided they know the circle area formula $A = \pi r^2$.

Start with a x-y coordinate plane, draw a circle at the center with radius 5. Show them the radius is 5 by drawing a line from (0,0) to (5,0). What's the area? $25\pi$. Now make the radius 4: draw your line from (0,0) to (4,0). Area is now $16\pi$. Then make the area 3, then 2, then 1, then 0, then...keep going...to -1! The circle shows up again! After shrinking to area 0, it starts growing again as the radii get more negative. You can show them the "radius" is -1 because you draw a "radius line" from 0 to -1. But the area of the circle is $\pi$. Because $\pi \times (-1)^2 = \pi$.

So finding the area with a "negative radius" (yeah, yeah, I know lengths should be positive, but the middle schoolers might enjoy the shrinkage from "positive radii" to "negative radii".) It looks cool, at any rate, and it motivates the fact that areas are still positive even when the lengths (okay, displacements) are negative.

Okay now for the fun part. Focus not in decreasing radii, but on decreasing area! Draw your circle with radius $25\pi$ then $16\pi$ then $9\pi$ then $4\pi$ then $\pi$ then $0\pi$ then ask them how to draw circles of areas $-\pi$, $-4\pi$, $-9\pi$ and so on. They won't be able to "see" those areas. The circle progression has gotten smaller and smaller but to make the areas negative the circles have to bounce back in another "dimension".

I have no idea whether middle schoolers will like this or not. But maybe, there is something here that says we can compute the radius for a negative area such as $$ A = -9\pi $$

using

$$ r = \sqrt{\frac{A}{\pi}} = \sqrt{\frac{-9\pi}{\pi}} = \sqrt{-9} = 3i $$

So the radius of this circle, which you cannot see, is "3 imaginary units"...3 units in...another dimension, the dimension of imaginary numbers. Maybe you can create an animation of the shrinking circle that pops out in another universe or something.

I don't know why that thought popped into my head, but felt it was okay to share. Something tells me there is a way to phrase it for middle schoolers.

Answer 10

I am not sure whether this counts but it may be useful.

There is a simple, well-known formula for solving quadratic equations. This is frequently useful.

There is a less well-known and more complex formula for cubic equations. One quirk of this is that you may need to take square roots of negative numbers even if they final answer is real. Today, mathematicians are quite relaxed about this step but they were once suspicious. A rerun of the Greeks and irrational numbers.

Cubic function at Wikipedia

Answer 11

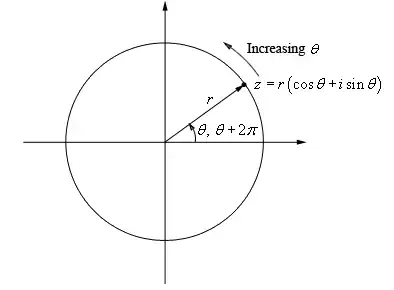
A complex number represents a rotation and a scaling and translation of another complex number.

That is about as physical as it gets in mathematics.

Given two complex numbers, a+b is translating a by b.

And a*b is rotating a by the angle of b, then scaling the result by the magnitude of b.

A strange thing happens because the same value b represents both a scaling/rotation operation, and a translation operation, on another complex number.

So how do we inspire that physically?

If we have:

(a + b)*c

this is obviously "start with a. Move by b. Then rotate/scale based on c. The algebra lets us break this apart:

a*c + b*c

which is really neat. There is a whole pile of things you can align this algebraic manipulation to physical operations here.

The next bit is a bit strange:

a * (b + c)

what happens when you add complex rotate-and-scale operations? Well, algebra tells us this is:

a*b + a*c

the operation b+c becomes "what if you took something, rotated it scaled by b and then by c, then added the result".

This is strange operation. But you know what isn't a strange operation?

(b * lambda + c * (1-lambda))

This is called an affine combination of b and c.

So we have two different rotation/scales, b and c. And we want to interpolate between them smoothly.

Then

a* (b * lambda + c * (1-lambda))

as lambda goes from 0 to 1 gives us the result of transforming a first by b, then finally by c, and having a smooth transformation in between.

Also

a * (b * c)

is rotate/scale a by b, then by c. b*c is the combination of the two rotations/scales in one value.

So applying the same rotation/scale twice would be:

a * (b*b)

or

a * b^2

which means that if c^2 = b, then

a*c^2 = a*b

or, c is the operation that if you do twice, you get b.

On the real line there are two different operations such that if you do either one twice, you get 4. They are -2 and 2. The same holds in the complex numbers.

Of interest is

a * c^3

because on the real line, there is only one scale factor that can get 8 if you do it 3 times. But in the complex numbers there are 3.

To see this, look at scaling by 1. On the real line, there are two scale/rotates that reach 1 by applying twice -- "-1" and "1". These correspond to the complex numbers 1 e^0 and 1 e^(pi i) -- no scale, no rotation, and no-scale, half rotation.

If you do half rotation twice, you get a full rotation, ie nothing.

How about the cube root of 1? Something you do 3 times that is a scale or rotation, and afterwards you end up being back where you started.

Answer 12

I can highly recommend section 5-2 of Eisberg and Resnick's Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles. I'll give a brief overview of the argument. I missed the part about middleschoolers in the OP. But this is a discussion that any high school student should be able to follow, and it shows why complex numbers are not just mathematically useful, but physically necessary.

In quantum mechanics, we study something called the wave function, which encodes the state of a quantum mechanical system (up to multiplication by a complex number). For a particle, the magnitude squared of the wave function determines the probability of finding a particle at a particular location. We want to know what equation describes the time evolution of the wave function. That is, we are seeking the analog of $F = m\ddot{x}$ for quantum mechanical states. From experimental data we know that for free particles the wave function can take the form $$ \psi(x,t) = A\cos(kx - \omega t) + B\sin(kx - \omega t) $$ where $A,B$ are some constants, $$ p = \hbar k $$ is the momentum of the particle, and $$ E = \hbar \omega $$ is the energy of the particle (these are known as the De Broglie relations). A free particle is just a particle which satisfies $$ E = \frac{p^2}{2m} $$ where $m$ is the mass of the particle. Substituting, we see that $$ \hbar \omega = \frac{\hbar^2 k^2}{2m} $$ Time derivatives of $\psi(x,t)$ bring out factors of $\omega$ and space derivatives of $\psi(x,t)$ bring out factors of $k$. Thus, the simplest differential equation for the wave function which will satisfy the above equation for our known solution $\psi(x,t)$ will involve a time derivative of the wave function and a second order space derivative of the wave function and nothing else. That is, we guess that the wave function of a free particle is given by a differential equation of the form $$ \alpha \frac{\partial \psi}{\partial t} + \beta \frac{\partial^2 \psi}{\partial x^2} = 0 $$ where we have introduced constants $\alpha$ and $\beta$ to take care of pesky factors of $m$ and $\hbar$. Upon substituting $\psi(x,t)$, we find $$ \alpha \left(A\omega \sin(kx - \omega t) - B\omega \cos(kx - \omega t) \right) + \beta \left( -Ak^2 \cos(kx - \omega t) - B k^2 \sin(kx - \omega t) \right) = 0 $$ This can only be satisfied for general $x$ and $t$ if \begin{align} \alpha A \omega - \beta B k^2 &= 0 \\ -\alpha B \omega - \beta A k^2 & = 0 \end{align} Adding $A$ times the first equation to $-B$ times the second, we obtain $$ \alpha A^2 \omega + \alpha B^2 \omega = 0 $$ or $$ A^2 = -B^2 $$ There is no pair of real numbers $A$ and $B$ which can satisfy $A^2 = -B^2$, so at least one of these numbers must be imaginary.

To summarize the argument, from the De Broglie relations and the equation for the energy of a free particle, we are led naturally to a differential equation for the wave function (up to some constants). This is not the only possible differential equation, but it is the simplest form that doesn't contradict the experimental data. By plugging a known solution into the differential equation, we find that we must allow the wave function to be complex.

You might wonder how we know $\psi(x,t)$ is a solution to a differential equation we have not yet determined. We know what $\psi(x,t)$ is in physical terms. $|\psi(x,t)|^2$ tells us the probability of detecting the particle at location $x$ at time $t$. Based on this interpretation and experimental evidence, we have seen that free particles must have wave functions that look like the $\psi(x,t)$ given above. Therefore, any equation that determines the wave function must admit $\psi(x,t)$ as a solution. Thus, if real $\psi(x,t)$ is not a solution to the differential equation, then either the equation is wrong, or $\psi(x,t)$ is not real. All the evidence we have so far tells us that the equation is right, so $\psi(x,t)$ must really be complex!

Answer 13

I was amazed when I realised for the first time that osclilating events, like sound waves, are best described and calculated by complex numbers. That was almost twenty years after I learned about them at school. That was also the first real-world application of complex numbers that I knew. My teachers failed to give us such an application. So at school, I never knew I would ever need them again...

Tell them what one can actually do with complex numbers outside the class room.

Answer 14

A physical example that should be comprehensible to bright 14 year olds. Fourier series and transforms can be used to describe functions and naturally produce complex numbers. I think complex numbers are easiest introduced by defining the solutions to $x^2+1=0$, analogously to negative numbers defining the solution to $x+1=0$. But it's good to have a physical example too.

Fourier series approximate periodic functions

Functions are ubiquitous in physics. Some functions can be periodic, for instance the red particles' positions as a function of time, $s(t)$, in the figure below.

Realistically, any function we observe will have some unexplained error. The red particles in the figure will not be moving perfectly back and forth due to other factors affecting their movement (e.g. buffeting about by the other particles).

So, if we wanted to interpolate $s(t)$ or find it's slope, we may want to approximate our periodic function with a simpler one. We would want to constrain this to a continuous function, since it is unrealistic for the particle to teleport through space. One natural choice is $\sin(t)$, since it's continuous and easy to define. But this doesn't quite solve the problem since $\sin(t)$ doesn't reflect the complex shape of $s(t)$. Hence, a sum of $\sin(t)$, with different amplitudes and frequencies could approximate $s(t)$ since it would have more potential for different shapes.*

The figure below shows what this looks like in practice, when we approximate the red $s(t)$ with the green sum of $\sin(t)$. The right amplitudes for each frequency of $\sin(t)$ are shown below. So we have successfully approximated a periodic function with a sum of $\sin(t)$ (Fourier series) that is easier to work with.

We can find explicit expressions for the amplitudes at each frequency that follows from the properties of $\sin$ and $\cos$. The proof might be slightly beyond your students' current skills but they could possibly go through it with a little help. Suffice it to say, we can look at the strength of each frequency in $s(t)$.

Fourier transforms generate complex numbers

The Fourier transform allows us to generalise this technique to approximate functions that are less obviously periodic (if at all) or to test whether they have periodicity. Just like with the Fourier series, we can say "how much" of each frequency makes up the function. This is particularly useful if we just want to describe the most important bits of our data. It's far easier to say "the red particle has a strong oscillation of $3\,\mathrm{Hz}$" than to describe its position at every single point in time.**

So, how does the Fourier transform find the strength of each frequency? We can't use the technique we used earlier with the Fourier series, since we don't know how our function is periodic. In order to proceed, we can describe the frequency of each wave that makes up the function by a certain strength (magnitude). But we must also know the phase-offset since $\sin(t)$ could be present as $\sin(t+1)$.

What system of numbers incorporates both a magnitude and a phase? The complex numbers do. Not only does a complex number have a 'size' (modulus), it also has an 'angle' (argument). So each frequency, with a magnitude and phase-offset, is naturally associated with a complex number, with a modulus and argument (as in the figure below). Hence, this is the output of the Fourier transform, if we adapt our earlier technique for Fourier series coefficients. This also requires some slightly difficult calculus.

Hence, complex numbers (via Fourier transforms) allow us to describe data with some semblance of "waves". This could be for physical waves (electromagnetic waves or wavefunctions) or abstract waves, such as relating the "frequencies" of the prime-counting function with the complex numbers of the Riemann zeta function.

To summarise, when we want to describe the important frequencies that make up a function, we must consider both the size and phase of each frequency, which corresponds with the modulus and argument of a complex number.

---

* The sum should include terms with both $\sin$ and $\cos$.

** This fact is the basis for .jpg and .mp3 file compression algorithms; another example of the utility of complex numbers.

Answer 15

Why not use space dimensions and cartesian coordinate frames to clarfy complex numbers? that is the most intuitive way to understand them that I came across when I was at middle school.

Imagine an ant in a 1-D world. The ant can travel only backwards or forwards and its position can be described by one real number x. In a parallel universe, we have ants living in a 2-D world. In this world, complex numbers can define a position of ants on a surface. A complex number x + iy describes an ant which traveled x front/rear and y sideways (left/right migh be easier for the kids to understand). And i is just there to indicate that that number describes movement on the second dimension.

Woudln't that satisfy the kids' imagination?

Edit: from this website about the history of complex numbers

Over decades, many people believed that complex numbers existed, and set out to make them understood and accepted. One of the ways they wanted to make them accepted was to be able to plot them of a graph. In this case, the X-axis is would be real numbers, and the Y-axis would be imaginary numbers. If the number were purely imaginary (like 2i), it would just be on the Y-axis. If the number was purely real, it would just be on the X-axis. The first person who considered this kind of graph was John Wallis. In 1685, he said that a complex number was just a point on a plane, but he was ignored. More than a century later, Caspar Wessel published a paper showing how to represent complex numbers in a plane, but was also ignored. In 1777, Euler made the symbol i stand for √-1, which made it a little easier to understand. In 1804, Abbe Buee thought about John Wallis’s idea about graphing imaginary numbers, and agreed with him. In 1806, Jean Robert Argand wrote how to plot them in a plane, and today the plane is called the Argand diagram. In 1831, Carl Friedrich Gauss made Argand’s idea popular, and introduced it to many people. In addition, Gauss took Descartes’ a+bi notation, and called this a complex number. It took all these people working together to get the world, for the most part, to accept complex numbers.

Answer 16

I don't know how seriously to take the suggestion, but the novel Smilla's Sense of Snow by Peter Høeg suggests that the crystal formation of ice is one such example. In one passage, the protagonist embarks on a long monologue about numbers:

Do you know what the foundation of mathematics is? The foundation of mathematics is numbers. If anyone asks me what makes me truly happy, I would say: numbers. Snow and ice and numbers. And do you know why? Because the number system is like human life. First you have the natural numbers. The ones that are whole and positive. The numbers of a small child. But human consciousness expands. The child discovers a sense of longing, and do you know what the mathematical expression is for longing ... The negative numbers. The formalization of the feeling that you are missing something. And human consciousness expands and grows even more, and the child discovers the in between spaces. Between stones, between pieces of moss on the stones, between people. And between numbers. And do you know what that leads to? It leads to fractions. Whole numbers plus fractions produce rational numbers. And human consciousness doesn't stop there. It wants to go beyond reason. It adds an operation as absurd as the extraction of roots. And produces irrational numbers ... It's a form of madness. Because the irrational numbers are infinite. They can't be written down. They force human consciousness out beyond the limits. And by adding irrational numbers to rational numbers, you get real numbers ... It doesn't stop. It never stops. Because now, on the spot, we expand the real numbers with the imaginary square roots of negative numbers. These are numbers we can't picture, numbers that normal human consciousness cannot comprehend. And when we add the imaginary numbers to the real numbers, we have the complex number system. The first number system in which it's possible to explain satisfactorily the crystal formation of ice. It's like a vast, open landscape. The horizons. You head toward them and they keep receding.

Whether or not it is scientifically accurate, I have found that this passage is a nice way to motivate the development of number systems. I often show the quote when I teach Survey of Math classes. If nothing else, it catches students' attention.

Answer 17

Not 100% sure if it is a good example, but afaik the time-dependent Schrödinger equation contains i (https://en.wikipedia.org/wiki/Schr%C3%B6dinger_equation#Time-dependent_equation).