The Euler method has the general error bound
$$
e(t,h)\le \frac{M}{2L}(e^{Lt}-1)h
$$
where $M$ is a bound on the second derivative of the solution or on the term $(f_t+f_xf)$ for the ODE function $f$ in the region that the solution curve lies in. $L$ is a Lipschitz constant of $f$ in the same region. For $t=h$ this reduces to the local quadratic truncation error $Mh^2$. This is a more specific statement of the general fact that the local truncation error order of the Euler method is 2, while the global error order is 1.
Your test problem
$$
y'=-2y^2-\frac{16y}{t+1}, ~~ y(2)=4, ~~ t\in[2,3], ~~ h=0.1\cdot 2^{-k}
$$
is a Bernoulli equation, which class has the general form
$$y'(t)=P(t)y(t)+Q(t)y^n.$$
The general solution method is to set $u=y^{1-n}$ to obtain a linear first order ODE. Here set $u=y^{-1}$, then
$$
u'=-y^{-2}y'=2 + \frac{16u}{t+1}\iff\left(\frac{u}{(t+1)^{16}}\right)'=\frac2{(t+1)^{16}}
\\
\implies \frac{u(t)}{(t+1)^{16}}-\frac{u(2)}{3^{16}}=\frac2{15}\left(\frac1{3^{15}}-\frac{1}{(t+1)^{15}}\right)
$$
Returning to the original equation one gets
$$
y(t)=-\frac{15}{2(t+1)(1-ϵ(t+1)^{15})}
$$
with $ϵ=\frac1{3^{15}}\left(\frac{5}{2y(2)}+1\right)=\frac1{3^{15}}\frac{13}8$ with the initial condition $y(2)=4$.
The exact solution is convex falling to zero, initially rapidly with $y'(2)=-\frac{160}3$, the tangents will lie below the curve, thus the Euler method will deviate from the exact solution towards the $t$-axis, possibly overshooting the constant solution $y=0$.
The high degree in the "perturbation" term $ϵ(t+1)^{15}$ will dominate the long-term behavior of solution and error. While initially the error will follow the exponential bound, for longer times it will behave like $t^{-16}$.
Performing the method with the given data results in the error table
h=1.000000e-01, err=2.7930460474e+00, err/h=27.930460
h=5.000000e-02, err=9.3880749525e-01, err/h=18.776150
h=2.500000e-02, err=3.1364679736e-01, err/h=12.545872
h=1.250000e-02, err=1.3673350606e-01, err/h=10.938680
h=6.250000e-03, err=6.4772632372e-02, err/h=10.363621
h=3.125000e-03, err=3.1568508260e-02, err/h=10.101923
h=1.562500e-03, err=1.5594241728e-02, err/h=9.980315
h=7.812500e-04, err=7.7506759066e-03, err/h=9.920865
h=3.906250e-04, err=3.8638549926e-03, err/h=9.891469
h=1.953125e-04, err=1.9290725518e-03, err/h=9.876851
h=9.765625e-05, err=9.6382466361e-04, err/h=9.869565
The first 5 lines for larger step sizes to indeed not exhibit typical first order behavior, the error quotients are close to 3. The asymptotic behavior of a first order method only manifests in the following lines that do not occur in the experiments in the question. There the error quotient between consecutive lines comes close to $2$ (or $0.5$ depending on the reading direction). As the dyadic power that one suspects inside the error is also contained in the step size. That the quotient of error and step size becomes constant around $9.85$ also shows compatibility with the global error order $1$.
Plotting the resulting solution curves on the left and the error divided by the step size $h$, that is, $e(t,h)/h$, on the right gives the following diagram.
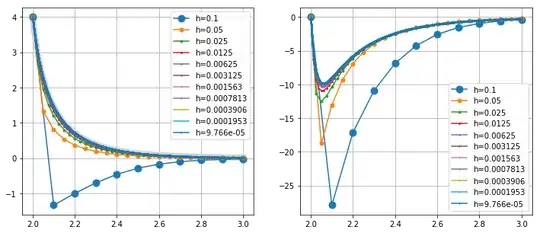
That the graphs on the right converge visually to one curve $c_1(t)$ shows that the error order is indeed 1.
